Bài tập 2. Hãy tìm số trung bình, tứ vị phân và mốt của các số liệu sau:

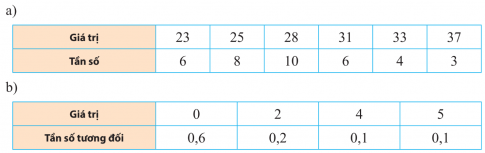
a. Số trung bình của mấu là: $\bar{x}$ = $\frac{1}{37}$(23 + 25 + 28 + 31 + 33 + 37) $\approx$ 4,78.

Cỡ mẫu là n = 37 là một số lẻ. Khi sắp xếp các số liệu theo thứ tự không giảm thì số liệu thứ 19 là 28. Do đó, giá trị tứ phân vị thứ hai là $Q_{2}$ = 28.

Tứ phân vị thứ nhất là trung vị của mẫu:

Cỡ mẫu là 18, là một số chẵn. Số liệu thứ 9 và 10 lần lượt là 25; 25. Do đó, giá trị tứ phân vị thứ nhất là $Q_{1}$ = $\frac{1}{2}$(25 + 25) = 25. 

Tứ phân vị thứ ba là trung vị của mẫu:

Cỡ mẫu là 18, là một số chẵn. Số liệu thứ 9 và 10 lần lượt là 31; 31. Do đó, giá trị tứ phân vị thứ ba là $Q_{3}$ = $\frac{1}{2}$(31 + 31) = 31.

Tần số của giá trị 28 là 10, lớn hơn tần số của các giá trị còn lại nên mẫu số liệu trên có $M_{0}$ = 28.

b. Số trung bình của mẫu là: $\bar{x}$ = $\frac{0 + 2 + 4 + 5}{0,6 + 0,2 + 0,1 + 0,1}$ = 11

Giá trị tứ phân vị thứ hai là $Q_{2}$ = $\frac{1}{2}$(0 + 0) = 0

Giá trị tứ phân vị thứ nhất là $Q_{1}$ = 0

Giá trị tứ phân vị thứ ba là $Q_{3}$ = 2

Tần số tương đối của giá trị 0 là 0,6, lớn hơn tần số tương đối của các giá trị còn lại nên mẫu số liệu trên có $M_{o}$ = 0