Bài tập 2.21. Giá trị lớn nhấ của biểu thức F(x; y) = 3x + y với (x; y) thuộc miền nghiệm của hệ...
Câu hỏi:
Bài tập 2.21. Giá trị lớn nhấ của biểu thức F(x; y) = 3x + y với (x; y) thuộc miền nghiệm của hệ bất phương trình 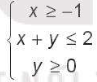 là
là
A. -3. B. 6. C. 5. D. 8.
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Huy
Phương pháp giải:Để tìm giá trị lớn nhất của biểu thức F(x; y) = 3x + y trong miền nghiệm của hệ bất phương trình, ta cần xác định miền nghiệm đó trước. Để xác định miền nghiệm, ta giải hệ các bất phương trình sau:1. x ≥ -12. x + y ≤ 23. y ≥ 0Từ bất phương trình 1, ta có đường thẳng d1: x = -1Từ bất phương trình 2, ta có đường thẳng d2: x + y = 2Từ bất phương trình 3, ta có đường thẳng d3: y = 0Miền nghiệm của hệ bất phương trình là miền tam giác với các đỉnh là (-1; 3), (-1; 0) và (2; 0).Tiếp theo, ta tính giá trị của F(x; y) tại các điểm cực đại của miền nghiệm:1. F(-1; 3) = 3*(-1) + 3 = 02. F(-1; 0) = 3*(-1) + 0 = -33. F(2; 0) = 3*2 + 0 = 6Vậy, giá trị lớn nhất của biểu thức F(x; y) trong miền nghiệm của hệ bất phương trình là 6, chọn đáp án B. 6.
Câu hỏi liên quan:
- Bài tập 2.10. Trong các bất phương trình sau, bất phương nào là bất phương trình bậc nhất hai ẩn?A....
- Bài tập 2.11. Trong các hệ bất phương trình sau, hệ bất phương trình nào hệ bất phương trình bậc...
- Bài tập 2.12. Điểm nào dưới đây thuộc miền nghiệm của bất phương trình 2x + 5y $\leq$ 10?A. (5;...
- Bài tập 2.13. Điểm nào dưới đây không thuộc miền nghiệm của bất phương trình 2x - 3y > 13?A. (1;...
- Bài tập 2.14. Cho bắt phương trình x + 2y < 3. Khẳng định nào sau đây là đúng?A. Miền nghiệm của...
- Bài tập 2.15. Cặp số nào dưới đây là nghiệm của bất phương trìnhA. (-1; 2). ...
- Bài tập 2.16. Điểm nào dưới đây thuộc miền nghiệm của hệ bất phương trìnhA. (-3; 2)....
- Bài tập 2.17. Miền nghiệm của hệ bất phương trình nào dưới đây là miền tam giác ABC (miền không bị...
- Bài tập 2.18. Miền nghiệm của hệ bất phương trìnhlàA. Một nửa mặt phẳng. ...
- Bài tập 2.19. Miền nghiệm của hệ bất phương trìnhlàA. Miền lục giác. B....
- Bài tập 2.20. Miền nghiệm của hệ bất phương trìnhlàA. Miền lục giác. B....
- Bài tập 2.22. Giá trị nhỏ nhất của biểu thức F(x; y) = -x + 4y với (x; y) thuộc miền nghiệm của hệ...
- Bài tập 2.23. Tổng của giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = x + 5y với (x;...
- Bài tập 2.24. Một hợp tác xã chăn nuôi dự định trộn hai loại thức ăn gia súc X và Y để tạo thành...
- Bài tập 2.25. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa...
- Bài tập 2.26. Biểu diễn miền nghiệm của các hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng...
- Bài tập 2.27. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y với (x;y)...
- Bài tập 2.28. Một phân xưởng có hai máy chuyên dụng $M_{1}$ và $M_{2}$ để sản xuất hai loại sản...
- Bài tập 2.29. Giả sử một người ăn kiêng cần được cụng cấp ít nhất 300 calo, 36 đơn vị vitamin A và...
Bình luận (0)





