Giải bài tập sách bài tập (SBT) toán lớp 10 kết nối tri thức bài 8 Tổng và hiệu của 2 vectơ
Hướng dẫn giải bài 8 Tổng và hiệu của 2 vectơ trang 48 sách bài tập (SBT) toán lớp 10 tập 1
Trong chương này của sách bài tập toán lớp 10, chúng ta sẽ tìm hiểu về cách tính tổng và hiệu của 2 vectơ. Bài toán này đưa ra một số vectơ và yêu cầu bạn tính tổng và hiệu của chúng.
Sách bài tập (SBT) toán lớp 10 tập 1 là một phần trong bộ sách "Kết nối tri thức" được thiết kế theo chương trình đổi mới của Bộ giáo dục. Nội dung trong sách được biên soạn một cách chi tiết và cụ thể, giúp học sinh nắm vững kiến thức một cách hiệu quả.
Chúng tôi hy vọng rằng, thông qua cách hướng dẫn và giải chi tiết trong bài tập này, học sinh sẽ hiểu rõ hơn về cách tính toán với vectơ và có khả năng áp dụng vào các bài toán khác trong tương lai.
Bài tập và hướng dẫn giải
Bài tập 4.7. Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ không cùng phương. Chứng minh rằng
$|\overrightarrow{a}| - |\overrightarrow{b}| < |\overrightarrow{a} + \overrightarrow{b}| < |\overrightarrow{a}| + |\overrightarrow{b}|$
Bài tập 4.8. Cho hình bình hành ABCD tâm O. M là một điểm tuỳ ý thuộc cạnh BC, khác B và C. MO cắt cạnh AD tại N.
a) Chứng minh rằng O là trung điểm MN.
b) Gọi G là trọng tâm tam giác BCD. Chứng minh rằng G cũng là trọng tâm tam giác MNC.
Bài tập 4.9. Cho tứ giác ABCD.
a) Chứng minh rằng $\overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CD} + \overrightarrow{DA} = \overrightarrow{0}$.
b) Chứng minh rằng $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{CD} + \overrightarrow{DA}$.
Bài tập 4.10. Cho tam giác ABC. Gọi D, E, F theo thứ tự là trung điểm của các cạnh BC, CA, AB.
a) Xác định vectơ $\overrightarrow{AF} - \overrightarrow{BD} + \overrightarrow{CE}$.
b) Xác định điểm M thoà mãn $\overrightarrow{AF} - \overrightarrow{BD} + \overrightarrow{CE} = \overrightarrow{MA}$.
c) Chứng minh rằng $\overrightarrow{MC} = \overrightarrow{AB}$.
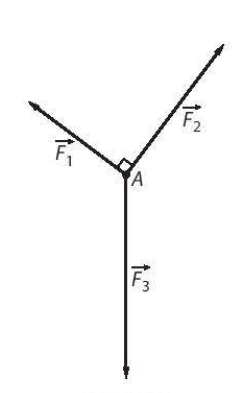
Bài tập 4.11. Trên Hình 4.7 biểu diễn ba lực $\overrightarrow{F_{1}}$, $\overrightarrow{F_{2}}$, $\overrightarrow{F_{3}}$ cùng tác động vào một vật ở vị trí cân bằng A. Cho biết |$\overrightarrow{F_{1}}$| = 30N, |$\overrightarrow{F_{2}}$| = 40N. Tính cường độ của lực $\overrightarrow{F_{3}}$.
Bài tập 4.12. Trên mặt phẳng, chất điểm A chịu tác dụng của ba lực $\overrightarrow{F_{1}}$, $\overrightarrow{F_{2}}$, $\overrightarrow{F_{3}}$ và ở trạng thái cân bằng. Góc giữa hai vectơ $\overrightarrow{F_{1}}$ và $\overrightarrow{F_{2}}$ bằng $60^{o}$. Tính độ lớn của $\overrightarrow{F_{3}}$, biết |$\overrightarrow{F_{1}}$| = |$\overrightarrow{F_{1}}$ = $2\sqrt{3}$N.





