Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây
Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây
Trong bài học này, chúng ta sẽ tìm hiểu về mối quan hệ giữa dây và khoảng cách từ tâm đến dây trên đường tròn. Hãy cùng nhau giải các bài toán sau để hiểu rõ hơn về vấn đề này.
A. HOẠT ĐỘNG KHỞI ĐỘNG
1. So sánh độ dài dây AB và CD trên mỗi hình 87 và giải thích.
Trong hình 87a, ta thấy AB > CD vì AB là đường kính của đường tròn, còn CD là dây cung.
Trong hình 87b, ta cũng thấy AB > CD.
2. Bài toán: Chứng minh rằng $OH^{2}$ + $HB^{2}$ = $OK^{2}$ + $KD^{2}$ khi cho AB và CD là hai dây của đường tròn (O; R).
Áp dụng định lý Py-ta-go vào các tam giác OHB và OKD, ta suy ra công thức $OH^{2}$ + $HB^{2}$ = $OK^{2}$ + $KD^{2}$.
B. HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC
1. Trong một đường tròn, hai dây bằng nhau thì cách đều tâm; hai dây cách đều tâm thì bằng nhau.
2. Trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn; dây nào gần tâm hơn thì dây đó lớn hơn.
3. So sánh độ dài ba cạnh của tam giác ABC khi O là giao điểm của ba đường trung trực và OH > OK > OI.
Do O là giao điểm của ba đường trung trực AB, AC, BC nên ta có AB < AC < BC do tính chất của dây trên đường tròn.
Để hiểu rõ hơn về mối quan hệ giữa dây và khoảng cách từ tâm đến dây trên đường tròn, hãy thực hành và giải thêm các bài tập liên quan. Chúc các em học tốt!
Bài tập và hướng dẫn giải
C. HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Trang 99 sách VNEN 9 tập 1
Cho đường tròn tâm O, bán kính 13cm, dây AB = 24cm.
a) Tính khoảng cách từ O đến đây AB.
b) Gọi M là điểm thuộc dây AB sao cho AM = 7cm. Kẻ dây EF đi qua M và vuông góc với AB. Chứng minh EF = AB.
Câu 2: Trang 100 sách VNEN 9 tập 1
Cho đường tròn (O) và một điểm E nằm ngoài đường tròn, vẽ đường tròn (E) cắt đường tròn (O) tại hai điểm A và B (h.91). Các đoạn thẳng EA và EB lần lượt cắt đường tròn (O) tại C và D (cho như hình vẽ). Chứng minh rằng hai dây AC và BD của đường tròn (O) bằng nhau.
Câu 3: Trang 100 sách VNEN 9 tập 1
Cho đường tròn (O) bán kính 2,5cm, dây AB = 4cm. Vẽ dây CD song song với AB và CD = 4,8cm. Tính khoảng cách giữa hai dây AB và CD.
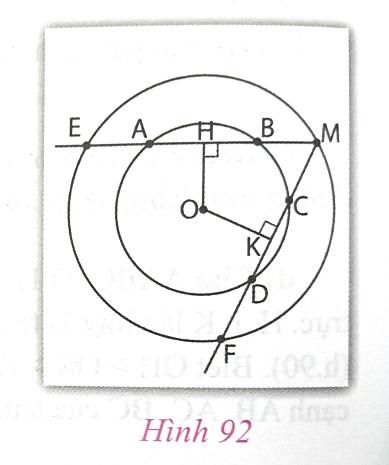
Câu 4: Trang 100 sách VNEN 9 tập 1
Cho hình 92, trong đó hai đường tròn cùng có tâm O. Cho biết AB > CD. Hãy so sánh các độ dài:
a) ME và MF;
b) MH và MK
D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNG
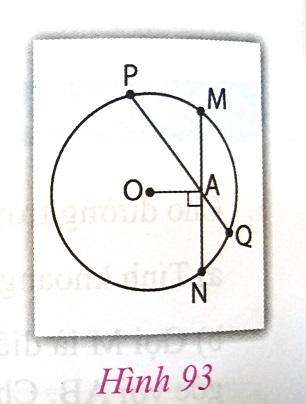
Câu 1: Trang 100 sách VNEN 9 tập 1
Cho đường tròn (O), điểm A nằm trong đường tròn. Vẽ dây MN vuông góc với OA tại A. Vẽ dây PQ bất kì đi qua A và không vuông góc với OA. Hãy so sánh độ dài hai dây MN và PQ (h.93)
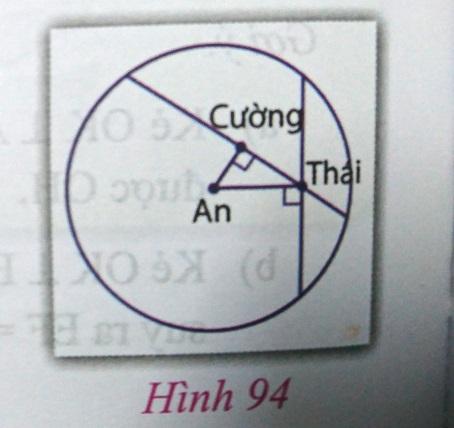
Câu 2: Trang 100 sách VNEN 9 tập 1
Đố: Nhà ba bạn An, Cường, Thái ở ba địa điểm như hình 94. Hỏi đoạn đường từ nhà An đến nhà Cường hay nhà Thái xa hơn? Vì sao?
Câu 3: Trang 101 sách VNEN 9 tập 1
Cho hình 95. Trên đường tròn (O) lấy hai dây AM và BN bằng nhau (M và N nằm trên cùng một nửa mặt phẳng bờ là đường thẳng AB). Hai đường thẳng AM và BN cắt nhau tại F. Chứng minh rằng:
a) OF là phân giác của góc AOB.
b) OF vuông góc với AB.