Luyện tập 2:Cho đường tròn có phuong trình x^2+ y^2= a^2và số (0 < k...
Câu hỏi:
Luyện tập 2: Cho đường tròn có phuong trình x^2 + y^2 = a^2 và số (0 < k < 1). Với mỗi điểm M(x0; y0) thuộc đường tròn, gọi H(x0; 0) là hình chiếu vuông góc của M lên trục Ox và N là điểm thuộc đoạn MH sao cho HN = kHM (H.3.5).
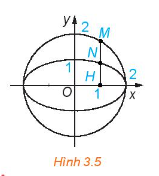
a, Tính toạ độ của N theo x0; y0; k.
b, Chứng minh rằng khi điểm M thay đổi trên đường tròn thì N thay đổi trên elip có phương trình chính tắc![]()
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Phương
Để giải câu hỏi trên, ta có thể thực hiện như sau:a, Gọi tọa độ của điểm N là (xN, yN). Với điểm M(x0, y0) thuộc đường tròn x^2 + y^2 = a^2 và điểm H(x0, 0) là hình chiếu vuông góc của M lên trục Ox, ta có HM = sqrt[(x0 - xN)^2 + y0^2] và HN = sqrt[(x0 - xN)^2 + yN^2]. Vì HN = kHM, ta có: sqrt[(x0 - xN)^2 + yN^2] = k * sqrt[(x0 - xN)^2 + y0^2].Bình phương hai vế ta được: (x0 - xN)^2 + yN^2 = k^2 * [(x0 - xN)^2 + y0^2].Suy ra: (1 - k^2) * (x0 - xN)^2 = k^2 * (y0^2 - yN^2).Từ đó ta có tọa độ của điểm N là: xN = x0 * (1 - k^2) / (1 + k^2) và yN = y0 * (1 + k^2) / (1 + k^2).b, Khi M thay đổi trên đường tròn x^2 + y^2 = a^2, ta có x0^2 + y0^2 = a^2. Từ phần a, ta đã tìm được tọa độ của điểm N theo x0, y0 và k. Thay x0^2 + y0^2 = a^2 vào tọa độ của N, ta sẽ thu được phương trình chính tắc của elip mà N thay đổi trên đó.Trả lời câu hỏi:a, Tọa độ của N là (xN, yN) với xN = x0 * (1 - k^2) / (1 + k^2) và yN = y0 * (1 + k^2) / (1 + k^2).b, Khi M thay đổi trên đường tròn, điểm N sẽ thay đổi trên elip có phương trình chính tắc là x^2 / (1 - k^2) + y^2 / (1 + k^2) = a^2.
Câu hỏi liên quan:
- Câu hỏi khởi động: Một hành tinh trong hệ Mặt Trời chuyển động theo một quỹ đạo hình elip nhận tâm...
- Luyện tập 1:Viết phương trình chính tắc của elip với độ dài trục lớn bằng 10 và tiêu cự bằng...
- 2.BÁN KÍNH QUA TIÊU CỰ, TÂM SAI VÀ ĐƯỜNG CHUẨNHoạt động 2: Cho hau tiêu điểm F1(-c;0), F2(c;0) và...
- Luyện tập 3: Cho elipđiểm M thay đổi trên elip. Hỏi khoảng cách từ M tới một tiêu điểm...
- Vận dụng 1: Với thông tin được đưa ra tronh tình huống mở đầu, lập phương trình chính tắc của elip...
- Hoạt động 3:Cho elip có phương trình chính tắcvới các tiêu điểm F1(–c; 0), F2(c; 0), ở...
- Luyện tập 4: Cho elip có phương trình chính tắcTìm tâm sai và các đường chuẩn của elip. Tính...
- Vận dụng 2: MặtTrăng chuyển động theo một quỹ đạo hình elip nhận tâm Trái Đất là một tiêu...
- BÀI TẬP3.1. Cho elipa) Xác định đỉnh và độ dài các trục của elip.b) Xác định tâm sai và các...
- 3.2.Viết phương trình chính tắc của elip trong mỗi trường hợp sau:a) Độ dài trục lớn bằng 8,...
- 3.3. Cho elipa,Qua tiêu điểm của elip vẽ đường thẳng vuông góc với trục Ox, cắt...
- 3.4.Đường tròn phụ của hình elip là đường tròn có đường kính là trục nhỏ của elip...
- 3.5.Với tâm sai khoảng 0,244, quỹ đạo elip của sao Diêm Vương "dẹt" hơn so với quỹ đạo của...
- 3.6.Một phòng thì thầm có trần vòm elip với hai tiêu điểm ở độ cao 1,6 m (so với mặt sàn) và...
Bình luận (0)





