Giải bài tập chuyên đề toán lớp 10 kết nối tri thức bài: Bài tập cuối chuyên đề 3
Hướng dẫn giải bài tập cuối chuyên đề 3 sách toán lớp 10 kết nối tri thức
Bài tập cuối chuyên đề 3 trang 61 trong sách toán lớp 10 kết nối tri thức là một phần quan trọng giúp học sinh nắm vững kiến thức. Hướng dẫn giải bài tập cụ thể và chi tiết sẽ cung cấp cho học sinh cái nhìn rõ ràng về cách giải các bài toán. Qua đó, giúp học sinh phát triển năng lực vận dụng tri thức một cách hiệu quả hơn.
Bộ sách này được biên soạn với mong muốn giúp đỡ học sinh hiểu bài học một cách toàn diện. Cách hướng dẫn trong sách giải bài tập cuối chuyên đề 3 trang 61 sẽ giúp học sinh tự tin hơn khi đối mặt với những bài toán khó khăn. Hy vọng rằng, qua việc giải bài tập này, học sinh sẽ có cơ hội rèn luyện và phát triển kỹ năng toán học của mình.
Bài tập và hướng dẫn giải
3.21. Cho conic (S) có tâm sai e = 2, một tiêu điểm F(–2; 5) và đường chuẩn tương ứng với tiêu điểm đó là Δ: x + y – 1 = 0. Chứng minh rằng, điểm M(x; y) thuộc đường conic (S) khi và chỉ khi x^2 + y^2 + 4xy – 8x + 6y – 27 = 0 (được gọi là phương trình của (S), tuy vậy không phải là phương trình chính tắc). Hỏi (S) là đường gì trong ba đường conic?
3.22. Viết phương trình đường conic có tâm sai ![]() một tiêu điểm F(–1; 0) và đường chuẩn tương ứng là Δ: x + y + 1 = 0. Cho biết conic đó là đường gì?
một tiêu điểm F(–1; 0) và đường chuẩn tương ứng là Δ: x + y + 1 = 0. Cho biết conic đó là đường gì?
3.23. Chứng minh rằng đồ thị của hàm số y = ax^2 + bx + c (a ≠ 0) là một parabol có tiêu điểm là ![]() và đường chuẩn là
và đường chuẩn là ![]()
3.24. Cho hai parabol có phương trình y2 = 2px và y = ax2 + bx + c (a ≠ 0). Chứng minh rằng nếu hai parabol đó cắt nhau tại bốn điểm phân biệt thì bốn điểm đó cùng nằm trên đường tròn ![]()
3.25. Cho elip có phương trình ![]() Viết phương trình đường thẳng đi qua điểm M(2; 1) và cắt elip tại hai điểm A, B sao cho MA = MB.
Viết phương trình đường thẳng đi qua điểm M(2; 1) và cắt elip tại hai điểm A, B sao cho MA = MB.
3.26. Một tàu vũ trụ nằm trong một quỹ đạo tròn và ở độ cao 148 km so với bề mặt Trái Đất (H.3.27). Sau khi đạt được vận tốc cần thiết để thoát khỏi lực hấp dẫn của Trái Đất, tàu vũ trụ sẽ đi theo quỹ đạo parabol với tâm Trái Đất là tiêu điểm; điểm khởi đầu của quỹ đạo này là đỉnh parabol quỹ đạo.
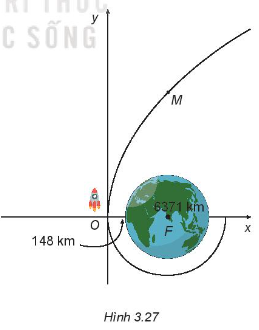
a) Viết phương trình chính tắc của parabol quỹ đạo (1 đơn vị đo trên mặt phẳng toạ độ ứng với 1 km trên thực tế, lấy bán kính Trái Đất là 6371 km ).
b) Giải thích vì sao, kể từ khi đi vào quỹ đạo parabol, càng ngày, tàu vũ trụ càng cách xa Trái Đất.





