Giải bài tập chuyên đề toán lớp 10 kết nối tri thức bài 7 parabol
Hướng dẫn giải chuyên đề parabol trang 54 sách toán lớp 10
Bài 7 trong sách chuyên đề toán lớp 10 kết nối tri thức là một bài toán về parabol. Bài toán này được biên soạn để giúp học sinh phát triển năng lực vận dụng tri thức của mình. Việc hướng dẫn và giải chi tiết bài toán này giúp học sinh hiểu rõ hơn về chủ đề parabol. Mong rằng, thông qua cách hướng dẫn cụ thể và giải chi tiết, học sinh sẽ có thể nắm vững bài học và áp dụng kiến thức một cách tốt nhất.
Bài tập và hướng dẫn giải
Câu hỏi khởi động: Hình ảnh parabol xuất hiện trong nhiều công trình kiến trúc đẹp. bác Vinh tham quan một công trình kiến trúc có cổng hình parabol với phương trình chính tắc y^2=48x ( theo đơn vị mét). Cổng rộng 192m. Bác dự định làm một mô hình thu nhỏ của nó với tỉ lệ 1:100. Liệu ta có thể giúp bác Vinh lập phương trình chính tắc cho Parabol ứng với mô hình đó, theo đơn vụ mét?
1. HÌNH DẠNG CỦA PARABOL
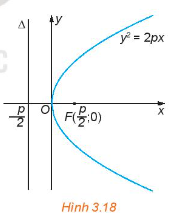
Hoạt động 1: Cho parabol có phương trình chính tắc y^2=2px (H.3.18)
a, Nếu điểm M(x0; y0) thuộc parabol thì điểm N(x0; –y0) có thuộc parabol hay không?
b, Từ phương trình chính tắc của parabol, có thể rút ra điều gì về hoành độ của những điểm thuộc parabol?
Luyện tập 1: Trong mặt phẳng tọa độ oxy, parabol (P) có phương trình chính tắc và đi qua điểm A(6; 6). Tìm tham số tiêu và phương trình đường chuẩn của (P).
2.BÁN KÍNH QUA TIÊU, TÂM SAI VÀ ĐƯỜNG CHUẨN
Hoạt động 2: Cho parabol có phương trình chính tắc y2 = 2px (H.3. 19).
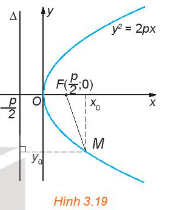
a) Nêu toạ độ tiêu điểm F và phương trình đường chuẩn Δ của parabol.
b) Cho điểm M(x0; y0) thuộc parabol. Hãy so sánh MF với d(M; Δ), từ đó, tính MF theo x0 và y0. Độ dài MF gọi là bán kinh qua tiêu của điểm M.
Luyện tập 2: Cho parabol có phương trình y^2 = 8x. Tìm toạ độ tiêu điểm và phương trình đường chuẩn của parabol. Tính bán kính qua tiêu của điểm M thuộc parabol biết điểm M có tung độ bằng 4.
Luyện tập 3: Một sao chổi chuyền động theo quỹ đạo parabol nhận tâm Mặt Trời làm tiêu điểm. Khoảng cách ngắn nhất từ sao chổi đến tâm Mặt Trời là 106 km. Lập phương trình chính tắc của quỹ đạo theo đơn vị kilômét. Hỏi khi sao chổi nằm trên đường vuông góc với trục đối xứng của quỹ đạo tại tâm Mặt Trời, thì khoảng cách từ sao chổi đến tâm Mặt Trời là bao nhiêu kilômét?
Vận dụng: Theo các bước sau, hãy giải quyết vấn đề đã được nêu ra ở phần mở đầu bài học.
a) Tìm chiều cao của cổng mà bác Vinh đã tham quan;
b) Tìm chiều cao và chiều rộng của mô hình thu nhỏ mà bác Vinh dự định làm;
c) Tìm phương trình chính tắc của mô hình đó, theo đơn vị mét;
d) Nếu tại tiêu điểm của mô hình, bác Vinh treo một ngôi sao thì ngôi sao đó ở độ cao bao nhiêu mét so với mặt đất?
BÀI TẬP
3.13. Cho parabol có phương trình y^2 = 12x. Tìm tiêu điểm và đường chuẩn của parabol. Tính bán kính qua tiêu của điểm M thuộc parabol và có hoành độ bằng 5.
3.14. Trong mặt phẳng toạ độ Oxy, parabol (P) có phương trình chính tắc và đi qua điểm 
. Tìm bán kính qua tiêu và khoảng cách từ tiêu điểm tới đường chuẩn của (P).
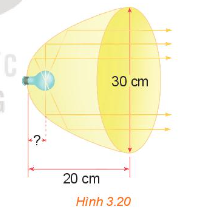
3.15. Xét đèn có bát đáy parabol với kích thước được thể hiện trên Hinh 3.20. Dây tóc bóng đèn được đặt ở vị trí tiêu điểm. Tính khoảng cách từ dây tóc tới đỉnh bát đáy.
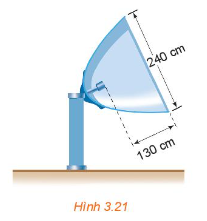
3.16. Anten vệ tinh parabol ở Hình 3.21 có đầu thu đặt tại tiêu điểm, đường kính miệng enten là 240 cm, khoảng cách từ vị tri đặt đầu thu tới miệng anten là 130 cm. Tính khoảng cách từ vị trí đặt đầu thu tới đỉnh anten.
