Giải bài tập sách bài tập (SBT) toán lớp 7 Kết nối tri thức bài 16 Tam giác cân. Đường trung trực của đoạn thẳng
Hướng dẫn giải bài 16 Tam giác cân
Trong sách bài tập toán lớp 7, mục bài tập 16 về tam giác cân được giải chi tiết trên trang 68. Bài toán này là một phần của chuỗi bài tập trong bộ sách "Kết nối tri thức" theo chương trình đổi mới của Bộ giáo dục. Bài toán này giúp học sinh rèn luyện kỹ năng giải bài toán, vận dụng kiến thức về đường trung trực của đoạn thẳng và tính chất của tam giác cân.
Cách hướng dẫn trong sách rất cụ thể và dễ hiểu, giúp học sinh nắm vững bài học. Bằng cách làm bài tập này, học sinh sẽ phát triển khả năng tư duy logic, suy luận và giải quyết vấn đề. Việc giải chi tiết bài toán cũng giúp học sinh hiểu rõ hơn về tính chất của tam giác cân và đường trung trực của đoạn thẳng.
Chúng ta cần dành thời gian và công sức để ôn tập và hiểu bài này một cách kỹ lưỡng. Việc nắm vững kiến thức toán học sẽ giúp học sinh tự tin hơn khi giải các bài toán khó hơn trong tương lai. Hy vọng rằng thông qua việc giải bài tập này, học sinh sẽ củng cố kiến thức toán học và phát triển khả năng giải quyết vấn đề.
Bài tập và hướng dẫn giải
BÀI TẬP
4.41. Trong những tam giác dưới đây (H.4.46), tam giác nào là tam giác cân, cân tại đỉnh nào? Vì sao?
4.42. Tính số đo các góc còn lại trong các tam giác cân dưới đây (H.4.47).
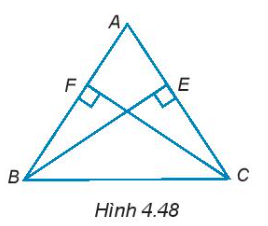
4.43. Tam giác ABC có hai đường cao BE và CF bằng nhau (H.4.48). Chứng minh rằng tam giác ABC cân tại đỉnh A.
4.44. Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
a) Tam giác ABD vuông tại B.
b)$ \Delta ABD=\Delta BAC$
c) Các tam giác AMB, AMC là các tam giác cân tại đỉnh M.
4.45. Cho tam giác ABC là tam giác cân đỉnh A. Chứng minh rằng:
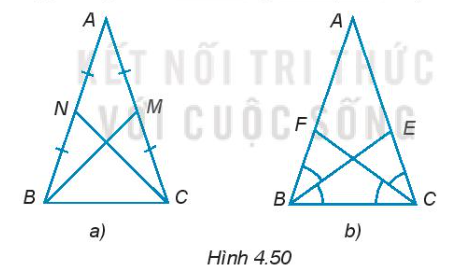
a) Hai đường trung tuyến BM, CN bằng nhau (H.4.50a).
b) Hai đường phân giác BE, CF bằng nhau (H.4.50b).
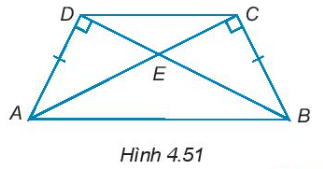
4.46. Cho các điểm A, B, C, D, E như hình 4.51. Chứng minh rằng:
a) $\Delta AEB$ và $\Delta DEC$ là các tam giác cân đỉnh E.
b) AB//CD
4.47. Cho tam giác ABH vuông tại đỉnh H có $\widehat{ABH}=60^{\circ}$. Trên tia đối của tia HB lấy điểm C sao cho HB = HC (H.4.52). Chứng minh rằng ∆ABC là tam giác đều và BH =$\frac{AB}{2}$
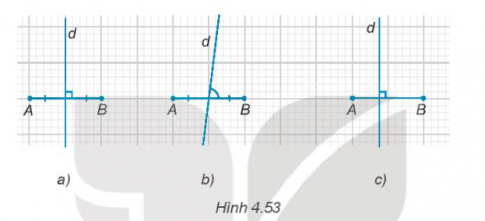
4.48. Đường thẳng d trong hình nào dưới đây là trung trực của đoạn thẳng AB?
4.49. Cho A là một điểm tùy ý nằm trên đường trung trực của đoạn thẳng BC sao cho A không thuộc BC. Khẳng định nào sau đây là đúng?
a) AB=AC.
b) Tam giác ABC đều.
c) $\widehat{ABC}=\widehat{ACB}$.
d) Tam giác ABC cân tại đỉnh A.
4.50. Cho tam giác ABC cân tại đỉnh A có đường cao AH. Cho M là một điểm tùy ý trên đường thẳng AH sao cho M không trùng với A (H.4.54). Chứng minh rằng: $\widehat{MBA}=\widehat{MCA}$
