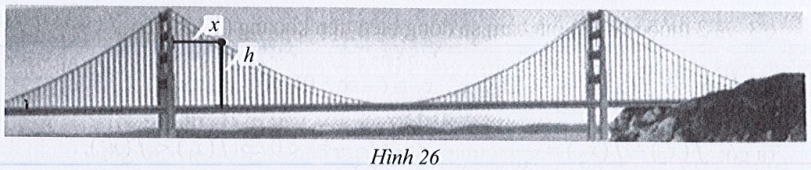
Bài 54 :Quan sát chiếc Cổng Vàng (Golden Gate bridge) ở Hình 26. Độ cao h (feet) tính từ mặt...

Bài 54 : Quan sát chiếc Cổng Vàng (Golden Gate bridge) ở Hình 26. Độ cao h (feet) tính từ mặt cầu đến các điểm trên dây treo ở phần giữa hai trụ cầu được xác định bởi công thức h(x) = 

19  000x2−715x+500">19  000x2−715x+500">19  000x2−715x+500">19  000x2−715x+500">19  000x2−715x+500">1/19  000x2−715x+500">19  000x2−715x+500">9 19  000x2−715x+500">00019  000x2−715x+500">19  000x2−715x+500">x2 19  000x2−715x+500">− 19  000x2−715x+500">19  000x2−715x+500">19  000x2−715x+500">19  000x2−715x+500">19  000x2−715x+500">7/19  000x2−715x+500">1519  000x2−715x+500">19  000x2−715x+500">19  000x2−715x+500">19  000x2−715x+500">x 19  000x2−715x+500">+ 19  000x2−715x+500">500, trong đó x(feet) là khoảng cách từ trụ cầu bên trái đến điểm tương ứng trên dây treo.

a) Xác định độ cao của trụ cầu so với mặt cầu theo đơn vị feet.

b) Xác định khoảng cách giữa hai trụ cầu theo đơn vị feet, biết rằng hai trụ cầu này có độ cao bằng nhau.