Giải bài tập toán lớp 11 kết nối tri thức bài 25 Hai mặt phẳng vuông góc

1. GÓC GIỮA HAI MẶT PHẲNG, HAI MẶT PHẲNG VUÔNG GÓC

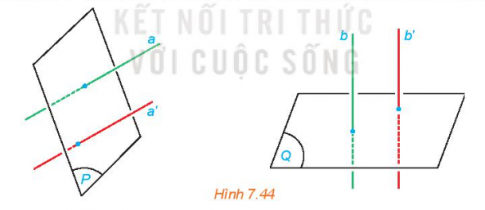
Hoạt động 1 trang 44 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hai mặt phẳng (P) và (Q). Lấy hai đường thẳng a, a' cùng vuông góc với (P), hai đường thẳng b, b' cùng vuông góc với (Q). Tìm mối quan hệ giữa các góc (a,b) và (a', b').

Luyện tập 1 trang 45 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hình chóp S.ABCD, đáy ABCD là một hình chữ nhật có tâm O, $SO \perp  (ABCD)$. Chứng minh rằng hai mặt phẳng (SAC) và (SBD) vuông góc với nhau khi và chỉ khi ABCD là một hình vuông.

2. ĐIỀU KIỆN HAI MẶT PHẲNG VUÔNG GÓC

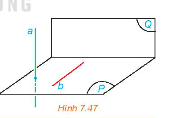
Hoạt động 2 trang 45 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho mặt phẳng (P) chứa đường thẳng b vuông góc với mặt phẳng (Q). Lấy một đường thẳng a vuông góc với (P) (H.7.47).

a) Tính góc giữa a và b.

b) Tính góc giữa (P) và (Q).

Luyện tập 2 trang 46 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Trong HĐ1 của Bài 23, ta đã nhận ra rằng đường thẳng nối các bán lề của của phòng vuông góc với sàn nhà. Hãy giải thích vì sao trong quá trình đóng – mở, cánh cửa luôn vuông góc với sàn nhà.

3. TÍNH CHẤT HAI MẶT PHẲNG VUÔNG GÓC

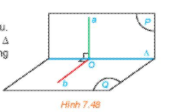
Hoạt động 3 trang 46 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Kẻ đường thẳng a thuộc (P) và vuông góc với giao tuyến $\Delta$ của (P)và (Q). Gọi O là giao điểm của a và $\Delta$. Trong mặt phẳng (Q), gọi b là đường thẳng vuông góc với $\Delta$ tại D.

a) Tính góc giữa a và b.

b) Tìm mỗi quan hệ giữa a và (Q)

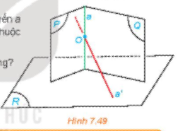
Hoạt động 4 trang 46 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến a cùng vuông góc với mặt phẳng (R). Gọi O là một điểm thuộc a và a' là đường thẳng qua O và vuông góc với (R).

a) Hỏi a có nằm trong các mặt phẳng (P). (Q) hay không?

b) Tim mối quan hệ giữa a và a'.

c) Tim mối quan hệ giữa a và (R).

Luyện tập 3 trang 47 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Với giả thiết như ở Ví dụ 3, chứng minh rằng:

a) Các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC);

b) Giao tuyển của hai mặt phẳng (AB'C'D') và (ABCD) là đường thẳng đi qua A, nằm trong mặt phẳng (ABCD) và vuông góc với AC.

4. GÓC NHỊ PHÂN

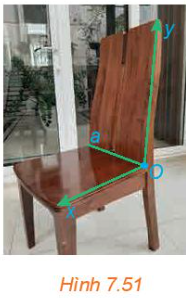
Hoạt động 5 trang 47 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Một tài liệu hướng dẫn rằng đối với ghế bàn ăn, nên thiết kế lưng ghế tạo với mặt ghế một góc có số đo từ 100° đến 105°. Trong Hình 7.51, các tia Ox, Oy được vẽ tương ứng trên mặt ghế, lưng ghế đồng thời vuông góc với giao tuyển a của mặt ghế và lưng ghế.

a) Theo tài liệu nói trên, góc nào trong hình nên có số đo từ 100° đến 105°?

b) Nếu thiết kế theo hướng dẫn đó thì góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế có thể nhận số đo từ bao nhiều đến bao nhiêu độ?

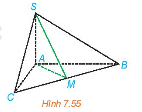
Luyện tập 4 trang 48 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hình chóp S.ABC có $SA \perp (ABC)$, AB = AC = a,

$\widehat{BAC}=120^{\circ}$ , $SA= \frac{a}{2\sqrt{3}}$. Gọi M là trung điểm của BC.

a) Chứng minh rằng SMA là một góc phẳng của góc nhị diện [S, BC, A].

b) Tinh số đo của góc nhị diện [S, BC, A].

Vận dụng 1 trang 48 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Trong cửa sổ ở Hình 7.56, cánh và khung cửa là các nửa hình tròn có đường kính 80 cm, bản lề được đính ở điểm chính giữa O của các cung tròn khung và cánh cửa. Khi cửa mở, đường kính của khung và đường kính của cánh song song với nhau và cách nhau một khoảng dị khi cửa đóng, hai đường kính đó trùng nhau. Hãy tính số đo của góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh, khung cửa khi d = 40 cm.

5. MỘT SỐ HÌNH LĂNG TRỤ ĐẶC BIỆT 

a) Hình lăng trụ đứng 

Hoạt động 6 trang 49 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Các mặt bên của lăng trụ đứng là các hình gì và các mặt bên đó có vuông góc với mặt đáy không? Vì sao?

b) Hình lăng trụ đều

Hoạt động 7 trang 49 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Các mặt bên của hình lăng trụ đều có phải là các hình chữ nhật có cùng kích thước hay không? Vì sao?

c) Hình hộp đứng

Hoạt động 8 trang 49 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Trong 6 mặt của hình hộp đứng, có ít nhất bao nhiêu mặt là hình chữ nhật? Vì sao?

d) Hình hộp chữ 

Hoạt động 9 trang 50 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: 

a) Hình hộp chữ nhật có bao nhiêu mặt là hình chữ nhật? Vì sao?

b) Các đường chéo của hình hộp chữ nhật có bằng nhau và cắt nhau tại trung điểm mỗi đường hay không? Vi sao?

e) Hình lập phương

Hoạt động 10 trang 50 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Các mặt của một hình lập phương là các hình gì? Vì sao?

Vận dụng 2 trang 50 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Từ một tấm tôn hình chữ nhật, tại 4 góc bác Hùng cắt bỏ đi 4 hình vuông có cũng kích thước và sau đó hàn gắn các mép tại các góc như Hình 7.65. Giải thích vì sao bằng cách đó, bác Hùng nhận được chiếc thùng không nắp có dạng hình hộp chữ nhật.

6. HÌNH CHÓP ĐỀU VÀ HÌNH CHÓP CỤT ĐỀU

Hoạt động 11 trang 51 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Tháp lớn tại Bảo tàng Louvre ở Paris (H.7.66) (với kết cấu kinh và kim loại) có dạng hình chóp với đây là hình vuông có cạnh bằng 34 m, các cạnh bên bằng nhau và có độ dài xấp xỉ 32,3 m (theo Wikipedia.org).

Giải thích vì sao hình chiếu của đỉnh trên đây là tâm của đáy tháp.

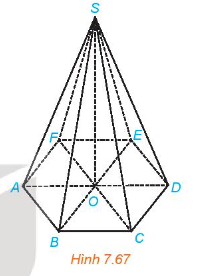
Hoạt động 12 trang 51 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hình chóp S.A₁A₂...A_n. Gọi O là hình chiếu của S trên mặt phẳng (A1A2...An).

a) Trong trường hợp hình chóp đã cho là đều, vị trí của điểm O có gì đặc biệt đối với tam giác đều A1A2...An?

b) Nếu đa giác A1A2...An là đều và O là tâm của đa giác đó thì hình chóp đã cho có gì đặc biệt?

Luyện tập 5 trang 51 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng $a\sqrt{\frac{5}{12}}$.Tính số đo của góc nhị diện [S, BC, A].

Hoạt động 13 trang 52 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hình chóp đều S.A₁A₂...A_n. Một mặt phẳng không đi qua S và song song với mặt phẳng đáy, cắt các cạnh SA1, SA2,.... SAn, tương ứng tai B1B2,....,B_n

a) Giải thích vì sao S.B1,B2,....,Bn, là một hình chóp đều.

b) Gọi H là tâm của đa giác A1A2...An. Chứng minh rằng đường thẳng SH đi qua tâm K của đa giác đều B1,B2,....,Bn, và HK vuông góc với các mặt phẳng (A1A2...An). (B1B2,....,Bn)

BÀI TẬP

Bài tập 7.16 trang 53 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hình chóp S.ABC có $SA \perp (ABC)$. Gọi H là hình chiếu của A trên BC.

a) Chứng minh rằng $(SAB) \perp (ABC)$ và $(SAH) \perp (SBC)$.

b) Giả sử tam giác ABC vuông tại A, $\widehat{ABC} = 30 ^{\circ}$, $AC = a$, $SA = \frac{a\sqrt{3}}{2}$ .Tính số đo nhị diện [S. BC. A]

Bài tập 7.17 trang 53 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.

a) Tính độ dài đường chéo của hình lập phương.

b) Chứng minh rằng $(ACC'A') \perp (BDD'B')$

c) Gọi O là tâm của hình vuông ABCD. Chứng minh rằng $\widehat{COC'}$ là một góc phẳng của góc nhị diện [C, BD, C']. Tinh (gần đúng) số đo của các góc nhị diện [C. BD, C]. [A, BD, C'].

Bài tập 7.18 trang 53 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hình hộp chữ nhật ABCD. A'B'C'D'.

a) Chứng minh rằng $(BDD'B') \perp (ABCD)$.

b) Xác định hình chiếu của $AC'$ trên mặt phẳng $(ABCD)$.

c) Cho $AB = a$,$BC=b$,$CC' =c$ . Tính $AC'$.

Bài tập 7.19 trang 53 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hình chóp đều S.ABC, đây có cạnh bằng a, cạnh bên bằng b.

a) Tính sin của góc tạo bởi cạnh bên và mặt đáy.

b) Tính tang của góc giữa mặt phẳng chứa mặt đáy và mặt phẳng chứa mặt bên.

Bài tập 7.20 trang 53 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Hai mái nhà trong Hình 7.72 là hai hình chữ nhật. Giả sử AB = 4,8m; OA = 2,8 m; OB = 4m.

a) Tính (gần đúng) số đo của góc nhị diện tạo bởi hai nửa mặt phẳng tương ứng chưa hai mái nhà.

b) Chứng minh rằng mặt phẳng (OAB) vuông góc với mặt đất phẳng. Lưu ý: Đường giao giữa hai mái (đường nóc) song song với mặt đất.

c) Điểm A ở độ cao (so với mặt đất) hơn điểm B là 0.5 m. Tính (gần đúng) góc giữa mái nhà (chứa OB) so với mặt đất.

Bài tập 7.21 trang 53 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Độ dốc của mái nhà, mặt sân, con đường thẳng là tang của góc tạo bởi mái nhà mặt sân, con đường thẳng đó với mặt phẳng nằm ngang. Độ dốc của đường thẳng dành cho người khuyết tật được quy định là không quá $\frac{1}{12}$ Hỏi theo đó, góc tạo bởi đường dành cho người khuyết tật và mặt phẳng nằm ngang không vượt quá bao nhiêu độ? (Làm tròn kết quả đến chữ số thập phân thứ hai).