Bài 30 :Dựa vào đồ thị hàm số bậc hai y = f(x) trong mỗi Hình 18a, 18b, 18c, hãy viết tập...
Câu hỏi:
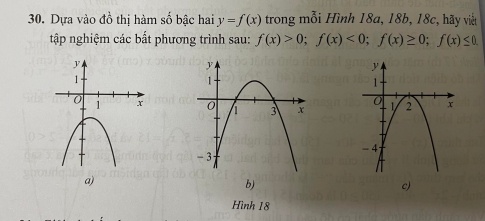
Bài 30 : Dựa vào đồ thị hàm số bậc hai y = f(x) trong mỗi Hình 18a, 18b, 18c, hãy viết tập nghiệm các bất phương trình sau: f(x) > 0; f(x) < 0; f(x) ≥ 0 và f(x) ≤ 0.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Linh
Để giải bài toán này, ta cần xác định vị trí của đồ thị hàm số y = f(x) đối với trục hoành (tức là xác định các điểm cắt trục hoành và hướng lên hoặc xuống). Sau đó, áp dụng các điều kiện f(x) > 0, f(x) < 0, f(x) ≥ 0, f(x) ≤ 0 để xác định tập nghiệm của các bất phương trình.Câu trả lời cho câu hỏi trên có thể được viết một cách chi tiết hơn như sau:- Xét hình 18a: đồ thị hàm số không cắt trục hoành, do đó tất cả các bất phương trình f(x) > 0, f(x) < 0, f(x) ≥ 0, f(x) ≤ 0 đều vô nghiệm.- Xét hình 18b: đồ thị hàm số nằm trên trục hoành trong khoảng (1; 3) và nằm dưới trục hoành trong khoảng (-∞; 1) và (3; +∞). Do đó, tập nghiệm của các bất phương trình sẽ là (1; 3), (-∞; 1) ∪ (3; +∞), [1; 3], (-∞; 1] ∪ [3; +∞) tương ứng.- Xét hình 18c: đồ thị hàm số cắt trục hoành tại x = 2 và nằm dưới trục hoành trừ tại x = 2. Do đó, tập nghiệm của các bất phương trình sẽ là ∅, ℝ \ {2}, {2}, ℝ tương ứng.Hy vọng bạn hiểu được cách giải và có thể tự giải câu hỏi này.
Câu hỏi liên quan:
- Bài 28 :Trong các bất phương tình sau, bất phương trình nào không là bất phương trình bậc...
- Bài 29 :Tập nghiệm của bất phương trình– x2+ 3x + 18 ≥ 0 là:A. [ – 3; 6].B....
- Bài 31 :Giải các bất phương trình bậc hai sau:a) 3x2– 8x + 5 > 0.b) – 2x2– x +...
- Bài 32 :Tìm giao các tập nghiệm của hai bất phương trình – 3x2+ 7x + 10 ≥ 0 và –...
- Bài 33 :Tìm m để phương trình – x2+ (m + 2)x + 2m – 10 = 0 có nghiệm.
- Bài 34 :Xét hệ tọa độ Oth trong mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng...
- Bài 35 :Một tình huống trong huấn luyện pháo binh được mô tả như sau: Trong mặt phẳng tọa độ...
Bình luận (0)





