Bài 28.Cho góc xOy. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD. Vẽ một...
Câu hỏi:
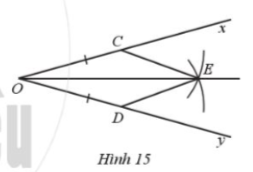
Bài 28. Cho góc xOy. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD. Vẽ một phần đường tròn tâm C và tâm D có cùng bán kính, E là điểm chung của hai phần đường tròn đó (E nằm trong góc xOy) (Hình 15). Vẽ các đoạn thẳng CE, DE. Chứng minh:
a) $\Delta OCE=\Delta ODE$.
b) OE là tia phân giác góc xOy.
c) $\widehat{OCE}=\widehat{ODE}$
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Đức
Để chứng minh phần a, ta có:- Ta có tam giác OCE và tam giác ODE đều có cạnh OC bằng OD (điều đã cho) và cạnh CE bằng DE (vì E là điểm chung của hai phần đường tròn cùng bán kính). - Vì cả hai tam giác có cạnh chung OE nên theo trường hợp Hai cạnh và góc giữa chúng bằng nhau (c.c.c), ta có $\Delta OCE=\Delta ODE$.Để chứng minh phần b, ta có:- Vì $\Delta OCE=\Delta ODE$ nên góc $\widehat{COE}$ và góc $\widehat{DOE}$ là bằng nhau (vì các góc tương ứng bằng nhau trong các tam giác đồng dạng).- Vậy, OE là tia phân giác của góc xOy.Để chứng minh phần c, ta có:- Vì $\Delta OCE=\Delta ODE$ nên các góc tương ứng trong hai tam giác tương đương nhau.- Do đó, $\widehat{OCE}=\widehat{ODE}$.Vậy, ta đã chứng minh các phần a, b và c đề bài yêu cầu.
Câu hỏi liên quan:






Chứng minh bằng định lí Pitago. Ta có tam giác OCE và ODE là tam giác vuông tại C và D. Do OC = OD, CE = DE, nên theo định lí Pitago, ta có OE = OE. Từ đó, suy ra OE là tia phân giác của góc xOy.
Chứng minh bằng định lí đồng viên. Vì tam giác OCE = tam giác ODE và CE = DE, nên ta có hai tam giác đồng dạng. Do đó, OE là tia phân giác của góc xOy.
Chứng minh bằng các góc cùng nội tiếp. Gọi H là giao điểm của CE và OD. Ta có góc OCH = góc OCE (cùng nội tiếp trên cùng cạnh). Tương tự, góc ODH = góc ODE. Từ đó, ta suy ra góc OCE = góc ODE.
Chứng minh bằng cạnh và góc đối của tam giác. Ta có OC = OD (đề bài), CE = DE (cùng bán kính), và góc OCE = góc ODE (do có tứ giác OCEM và ODEM là tứ giác đều). Từ đó, ta suy ra tam giác OCE = tam giác ODE.