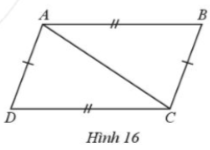
Bài 29.Ở hình 16 có AB = CD, AD = BC. Chứng minh:a) AB // CDb) $\widehat{ABC}=\widehat{ADC}$

a) Ta có:
- AB = CD (đề bài)
- BC = AD (đề bài)
- AC là đoạn chéo của hình chữ nhật

Do đó, từ hai tam giác ABC và CDA có cạnh và góc tương đồng, ta suy ra:
$\Delta ABC = \Delta CDA$ (c.c.c)
$\Rightarrow \widehat{BAC} = \widehat{ACD}$ (hai góc tương ứng)

Vì hai góc BAC và ACD ở vị trí so le trong nên ta kết luận được AB // CD.

b) Tương tự, từ $\Delta ABC = \Delta CDA$, ta suy ra:
$\widehat{ABC} = \widehat{ADC}$ (hai góc tương ứng)

Vậy, câu trả lời là:
a) AB // CD
b) $\widehat{ABC} = \widehat{ADC}$