4.3.Tìm các số đo góc x, y trong Hình 4.5.
Câu hỏi:
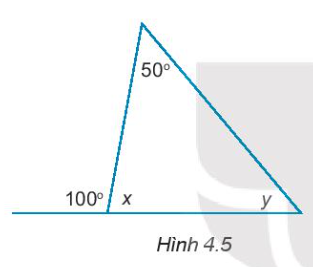
4.3. Tìm các số đo góc x, y trong Hình 4.5.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Linh
Để tìm số đo góc x và y trong Hình 4.5, ta có thể áp dụng định lý cung tròn và định lý góc đối và góc nhọn để giải bài toán.Phương pháp 1: Sử dụng định lý cung tròn- Vì góc nội tiếp trên cùng một cung có số đo bằng nhau, nên ta có: x = 180° - 100° = 80°- Góc y sẽ là góc đối diện với góc x, nên y = 180° - 80° - 50° = 50°Phương pháp 2: Sử dụng định lý góc đối và góc nhọn- Vì góc 50° là góc nhọn trong tam giác, nên góc đối với góc 50° cũng sẽ là 50°.- Do cùng thuộc tam giác, nên tổng các góc bằng 180°. Từ đó, ta có: x = 180° - 100° = 80°Vậy số đo góc x là 80° và số đo góc y là 50°.
Câu hỏi liên quan:
- BÀI TẬP4.1. Hãy tính các số đo các góc A, D, N trong tam giác dưới đây (H.4.3). Trong các tam...
- 4.2.Trong tam giác dưới đây (H.4.4), tam giác nào là nhọn, vuông, tù?
- 4.4.Tìm số đo các góc B và C của tam giác ABC trong Hình 4.6.
- 4.5.Tìm số đo góc x trong Hình 4.7.
- 4.6.Hãy viết các góc $\widehat{A},\widehat{B},\widehat{C}$ của tam giác ABC theo thứ tự tăng...
- 4.7.Hãy viết các góc $\widehat{A},\widehat{B},\widehat{C}$ của tam giác ABC theo thứ tự giảm...
- 4.8. Tính tổng số đo $\widehat{A}+\widehat{C}$ trong Hình 4.8.
- 4.9.Cho tam giác ABC thỏa mãn $\widehat{A}=\widehat{B}=2\widehat{C}$.a) Tính số đo các góc...





Áp dụng công thức tổng của các góc trong tam giác, ta có x + y + 90 = 180 do đó x + y = 90. Vậy góc x và y lần lượt là 45 độ
Sử dụng tính chất tứ giác đều, ta biết rằng tổng 4 góc bên của một hình tứ giác đều là 360 độ. Do đó, x + y + 90 + 90 = 360. Từ đó, suy ra giá trị của x và y
Ta có hệ phương trình x + y = 180 và x = 2y. Giải hệ phương trình này ta sẽ tìm được giá trị của x và y
Góc x và y là góc đối của nhau, tức là x + y = 180 độ