Giải bài tập sách bài tập (SBT) toán lớp 10 Cánh diều bài 1 Tọa độ của vectơ

BÀI TẬP

1. Tọa độ của vectơ $\vec{u}=-3\vec{i}+2\vec{j}$ là:

A. (-3; 2)

B. (2; -3)

C. $(-3\vec{i};2\vec{j})$

D. (3; 2)

2. Tọa độ của vectơ $\vec{u}=5\vec{j}$ là:

A. (5; 0)

B. $(5;\vec{j})$

C. $(0;5\vec{j})$

D. (0; 5)

3. Trong mặt phẳng tọa độ Oxy, cho A(2; - 5). Tọa độ của vectơ $\overrightarrow{OA}$ là:

A. (2; 5)

B. (2; -5)

C. (-2; -5)

D. (-2; 5)

4. Trong mặt phẳng tọa độ Oxy, cho A(- 1; 3), B(2; - 1). Tọa độ của vectơ $\overrightarrow{AB}$  là:

A. (1; -4)

B. (-3; 4)

C. (3; -4)

D. (1; -2)

5. Trong mặt phẳng tọa độ Oxy, cho $\overrightarrow{u}=(-2;-4),\overrightarrow{v}=(2x-y;y)$. Hai vecto $\overrightarrow{u}$ và $\overrightarrow{v}$ bằng nhau nếu:

A.$\left\{\begin{matrix}x=1\\ y=-4 \end{matrix}\right.$

B. $\left\{\begin{matrix}x=-3\\ y=-4 \end{matrix}\right.$

C. $\left\{\begin{matrix}x=1\\ y= 4\end{matrix}\right.$

D. $\left\{\begin{matrix}x=-3\\ y=4 \end{matrix}\right.$

6. Cho hình bình hành ABCD có A(- 1; - 2), B(3; 2), C(4; - 1). Tọa độ của đỉnh D là:

A. (8; 3)

B. (3; 8)

C. (-5; 0)

D. (0; -5)

7. Tìm tọa độ của các vectơ trong Hình 4.

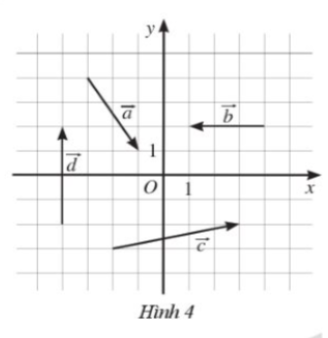
8. Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau:

a) $\overrightarrow{m}=(2a+3;b-1)$ và $\overrightarrow{n}=(1;-2)$

b) $\overrightarrow{u}=(3a-2;5)$ và $\overrightarrow{v}=(5;2b+1)$

c) $\overrightarrow{x}=(2a+b;2b)$ và $\overrightarrow{y}=(3+2b;b-3a)$

9. Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(- 4; 2), B(2; 4), C(8; - 2). Tìm tọa độ của điểm D sao cho tứ giác ABCD là hình bình hành.

10. Trong mặt phẳng tọa độ Oxy, cho tứ giác ABCD có A(xA; yA); B(xB; yB); C(xC; yC); D(xD; yD). Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi xA + xC = xB + xD và yA + yC = yB + yD

11. Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng M(1; - 2), N(3; 1), P(- 1; 2). Tìm tọa độ điểm Q sao cho tứ giác MNPQ là hình thang có MN // PQ và PQ = 2MN.