Giải bài tập chuyên đề toán lớp 10 cánh diều bài 2 Nhị thức Newton
Hướng dẫn giải bài 2 Nhị thức Newton trong sách Giải bài tập chuyên đề toán lớp 10 cánh diều
Trong trang sách chuyên đề toán lớp 10 cánh diều, bài 2 Nhị thức Newton trang 31 được giải chi tiết và cụ thể. Được biên soạn nhằm hỗ trợ học sinh phát triển năng lực vận dụng trí thức, cung cấp cách hướng dẫn dễ hiểu và chi tiết để các em có thể nắm vững bài học. Mong rằng, thông qua sách này, học sinh sẽ tiếp cận và hiểu sâu hơn về chuyên đề này.
Bài tập và hướng dẫn giải
I. Công thức nhị thức Newton
Hoạt động 1.
a) Chọn số thích hợp cho ? trong khai triển biểu thức sau:
$(a+3)^{3}=C_{3}^{?}a^{3-?}+C_{3}^{?}a^{3-?}b^{1}+C_{3}^{?}a^{3-?}b^{2}+C_{3}^{?}a^{3-?}b^{3}$
Từ đó nêu dạng tổng quát của mỗi số hạng trong khai triển biểu thức $(a + b)^{3}$.
b) Xét biểu thức $(a + b)^{n}$.
Nêu dự đoán về dạng tổng quát của mỗi số hạng trong khai triển biểu thức $(a + b)^{n}$.
Luyện tập 1. Khai triển biểu thức $(x + 2)^{7}$.
Luyện tập 2. Cho n ∈ ℕ*. Chứng minh $C_{n}^{0}+C_{n}^{1}+C_{n}^{2}+...+C_{n}^{n-1}+C_{n}^{n}=2^{n}$
II. Tam giác Pascal
Hoạt động 2.
Ta đã biết:
$(a+b)^{2}=C_{2}^{0}a^{2}+C_{2}^{1}ab+C_{2}^{2}b^{2}$
$(a+b)^{3}=C_{3}^{0}a^{3}+C_{3}^{1}a^{2}b+C_{3}^{2}ab^{2}+C_{3}^{3}b^{3}$
$(a+b)^{4}=C_{4}^{0}a^{4}+C_{4}^{1}a^{3}b+C_{4}^{2}a^{2}b^{2}+C_{4}^{3}ab^{3}+C_{4}^{4}b^{4}$
$(a+b)^{5}=C_{5}^{0}a^{5}+C_{5}^{1}a^{4}b+C_{5}^{2}a^{3}b^{2}+C_{5}^{3}a^{2}b^{3}+C_{5}^{4}ab^{4}+C_{5}^{5}b^{5}$
Ta sắp xểp những hệ số tổ hợp ở trên như sau:
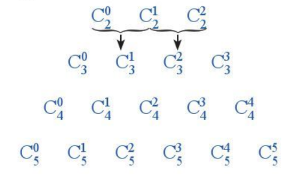
Nêu phép toán để từ hai số hạng của dòng trên suy ra được số hạng tương ứng (thể hiện ở mũi tên ↓) ở dòng dưới trong bảng các hệ số nói trên.
Luyện tập 3. Sử dụng tam giác Pascal để khai triển:
a) $(x + y)^{7}$;
b) $(x – 2)^{7}$.
III. Hệ số trong khai triển nhị thức Newton
1. Sự biến thiên của dãy hệ số trong khai triển nhị thức $(a+b)^{n}$
Hoạt động 3. Xét dãy các hệ số trong khai triển nhị thức $(a + b)^{4}$ ( Hình 7a) và nhị thức $(a + b)^{5}$ (Hình 7b) sau:

a) So sánh từng cặp hệ số $C_{4}^{0}$ và $C_{4}^{4};C_{4}^{1}$ và $C_{4}^{3}$ ở Hình 7a.
So sánh từng cặp hệ số $C_{5}^{0}$ và $C_{5}^{5};C_{5}^{1}$ và $C_{5}^{4};C_{5}^{2}$ và $C_{5}^{3}$ ở Hình 7b.
b) Nêu nhận xét về sự tăng giảm của mỗi dãy hệ số:
$C_{4}^{0} C_{4}^{1} C_{4}^{2} C_{4}^{3} C_{4}^{4}$ (trong khai triển (a + b)$^{4}$)
$C_{5}^{0} C_{5}^{1} C_{5}^{2} C_{5}^{3} C_{5}^{4} C_{5}^{5}$ (trong khai triển (a + b)$^{5}$)
Luyện tập 4. Tìm hệ số lớn nhất trong khai triển của:
a) (a + b)$^{2022}$;
b) (a + b)$^{2023}$.
2. Hệ số của x$^{k}$ trong khai triển (ax+b)$^{n}$ thành đa thức
Hoạt động 4. Quan sát khai triển nhị thức:
$(ax+b)^{n}=C_{n}^{0}(ax)^{n}+C_{n}^{1}(ax)^{n-1}b+C_{n}^{2}(ax)^{n-2}b^{2}+...+C_{n}^{n-1}(ax)b^{n-1}+C_{n}^{n}b^{n}$
$=C_{n}^{0}a^{n}x^{n}+C_{n}^{1}a^{n-1}bx^{n-1}+C_{n}^{2}a^{n-2}b^{2}x^{n-2}+...+C_{n}^{n-1}ab^{n-1}x+C_{n}^{n}b^{n}$
Nêu công thức tính của $x^{k}$ trong khai triển trên.
Luyện tập 5. Xét khai triển của (x + 5)4^{15}$.
a) Nêu số hạng chứa x$^{7}$, từ đó nêu hệ số của x$^{7}$.
b) Nêu số hạng tổng quát trong khai triển nhị thức trên, từ đó nêu hệ số ak của x$^{k}$ với 0 ≤ k ≤ 15.
Bài tập
Bài tập 1. Khai triển các biểu thức sau:
a) (2x + y)$^{6}$;
b) (x – 3y)$^{6}$;
c) (x – 1)$^{n}$;
d) (x + 2)$^{n}$;
e) (x + y)$^{2n}$;
g) (x – y)$^{2n}$;
trong đó n lả số nguyên dương.
Bài tập 2. Tính
a) $S= C_{2022}^{0}9^{2022}+C_{2022}^{1}9^{2021}+...+C_{2022}^{k}9^{2022-k}+...+C_{2022}^{2021}9+C_{2022}^{2022}$
b) $T=C_{2022}^{0}4^{2022}-C_{2022}^{1}4^{2021}\times 3+...-C_{2022}^{2021}4\times 3^{2021}+C_{2022}^{2022}3^{2022}$
Bài tập 3. Chứng minh:
$C_{n}^{0}3^{n}+C_{n}^{1}3^{n-1}+...+C_{n}^{k}3^{n-k}+...+C_{n}^{n-1}3+C_{n}^{n}$
$=C_{n}^{0}+C_{n}^{1}3+...+C_{n}^{k}3^{k}+...+C_{n}^{n-1}3^{n-1}+C_{n}^{n}3^{n}$
với $0\leq k\leq n;k,n\in N$*
Bài tập 4. Xác định hệ số của:
a) x$^{12}$ trong khai triển của (x + 4)$^{30}$;
b) x$^{10}$ trong khai triển của (3 + 2x)$^{30}$;
c) x$^{15}$ và x$^{16}$ trong khai triển của $(\frac{2x}{3}-\frac{1}{7})^{51}$
Bài tập 5. Xét khai triển của $(x+\frac{5}{2})^{12}$
a) Xác định hệ số của x$^{7}$.
b) Nêu số hạng tổng quát trong khai triển nhị thức trên, từ đó nêu hệ số ak của x$^{k}$ với 0 ≤ k ≤ 12.
Bài tập 6. Xét khai triển của $(\frac{x}{2}+\frac{1}{5})^{21}$
a) Xác định hệ số của x1$^{10}$.
b) Nêu số hạng tổng quát trong khai triển nhị thức trên, tưr đó nêu hệ số ak của x$^{k}$ với 0 ≤ k ≤ 21.
Bài tập 7. Tìm hệ số lớn nhất trong khai triển của:
a) (a + b)$^{8}$;
b) (a + b)$^{9}$.
Bài tập 8. Chứng minh công thức nhị thức Newton bằng phương pháp quy nạp:
$(a+b)^{n}=C_{n}^{0}a^{n}+C_{n}^{1}a^{n-1}b+...+C_{n}^{n-1}ab^{n-1}+C_{n}^{n}b^{n}$ với n ∈ ℕ*.
Bài tập 9. Bằng phương pháp quy nạp, chứng minh:
a) $n^{5}$ – n chia hết cho 5 ∀ n ∈ ℕ*;
b) n$^{7}$ – n chia hết cho 7 ∀ n ∈ ℕ*.
Bài tập 10. Cho tập hợp A = {x1; x2; x3; ... ; xn} có n phần tử. Tính số tập hợp con của A.
Bài tập 11. Một nhóm gồm 10 học sinh tham gia chiến dịch Mùa hè xanh. Nhà trường muốn chọn ra một đội công tác có ít nhất hai học sinh trong những học sinh trên. Hỏi có bao nhiêu cách lập đội công tác như thế?
Bài tập 12. Để tham gia một cuộc thi làm bánh, bạn Tiến làm 12 chiếc bánh có màu khác nhau và chọn ra số nguyên dương chẵn chiếc bánh để cho vào một hộp trưng bày. Hỏi bạn Tiến có bao nhiêu cách để chọn bánh cho vào hộp trưng bày đó?
Bài tập 13. Bác Thành muốn mua quà cho con nhân dịp sinh nhật nên đã đến một cửa hàng đồ chơi. Bác dự định chọn một trong năm loại đồ chơi. Ở cửa hàng, mỗi loại đồ chơi đó chỉ có 10 sản phẩm khác nhau bày bán. Biết rằng nếu mua bộ trực thăng điều khiển từ xa, bác sẽ chỉ mua 1 sản phẩm; nếu mua bộ đồ chơi lego, bác sẽ mua 3 sản phẩm khác nhau; nếu mua bộ lắp ghép robot chạy bằng năng lượng mặt trời, bác sẽ mua 5 sản phẩm khác nhau; nếu mua rubik, bác sẽ mua 7 sản phẩm khác nhau; còn nếu mua mô hình khủng long, bác sẽ mua 9 sản phẩm khác nhau. Bác Thành có bao nhiêu cách chọn quà sinh nhật cho con?
Bài tập 14. Giả sử tính trạng ở một loài cây được quy định do tác động cộng gộp của n cặp alen phân li độc lập A1a1, A2a2, ..., Anan. Cho cây F1 dị hợp về n cặp alen giao phối với nhau. Tỉ lệ phân li kiểu hình của F2 là hệ số của khai triển nhị thức Newton (a + b)$^{2n}$, nghĩa là tỉ lệ phân li kiểu hình của F2 là $C_{2n}^{0}:C_{2n}^{1}:C_{2n}^{2}:...:C_{2n}^{2n-2}:C_{2n}^{2b-1}:C_{2n}^{2n}$
Cho biết một loài cây có tính trạng được quy định bởi tác động cộng gộp của 4 cặp alen phân li độc lập. Tìm tỉ lệ phân li kiểu hình của F2 nếu cây F1 dị hợp về 4 cặp alen giao phối với nhau.





