Giải bài tập chuyên đề toán lớp 10 cánh diều bài 3 Parabol
Hướng dẫn giải bài 3 chuyên đề Parabol trang 57 sách toán lớp 10 cánh diều
Bài toán Parabol là một trong những bài toán quan trọng trong môn toán. Để giúp học sinh hiểu rõ về chuyên đề này, sách giải bài tập chuyên đề toán lớp 10 cánh diều đã biên soạn cách hướng dẫn và giải chi tiết bài 3 trang 57. Nội dung sách được xây dựng nhằm phát triển năng lực vận dụng tri thức cho học sinh.
Qua cách hướng dẫn cụ thể và giải chi tiết của sách, học sinh sẽ có cơ hội nắm vững bài học và áp dụng kiến thức vào thực tế một cách hiệu quả. Sự thông tin chi tiết và dễ hiểu trong sách chắc chắn sẽ giúp học sinh tự tin hơn khi giải các bài tập liên quan đến Parabol. Hy vọng rằng bộ sách này sẽ là một công cụ hữu ích trong quá trình học tập của học sinh lớp 10.
Bài tập và hướng dẫn giải
I. Tính đối xứng của Parabol
Hoạt động 1. Trong mặt phẳng tọa độ Oxy, ta xét parabol (P) có phương trình chính tắc $y^{2} = 2px$ (p > 0) (Hình 19).
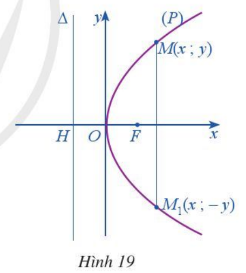
a) Tìm toạ độ tiêu điểm F của parabol (P).
b) Tìm toạ độ điểm H và viết phương trình đường chuẩn Δ của parabol (P).
c) Cho điểm M(x; y) nằm trên parabol (P). Gọi M1 là điểm đối xứng của M qua trục Ox. Điểm M1 có nằm trên parabol (P) hay không? Tại sao?
II. Tâm sai của Parabol. Bán kính qua tiêu của một điểm
Hoạt động 2. Trong mặt phẳng toạ độ Oxy, ta xét parabol (P) có phương trình chính tắc là $y^{2}$ = 2px (p > 0) (Hình 20).
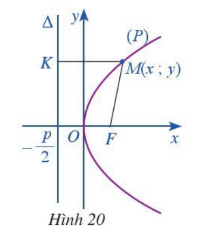
a) So sánh khoảng cách MF từ điểm M đến tiêu điểm F và khoảng cách MK từ điểm M đến đường chuẩn Δ.
b) Tính độ dài đoạn thẳng MK. Từ đó, tính độ dài đoạn thẳng MF.
Luyện tập 1.
a) Lập phương trình chính tắc của parabol (P), biết phương trình đường chuẩn là x = –2.
b) Tìm toạ độ tiêu điểm của parabol (P).
c) Tìm toạ độ điểm M thuộc parabol (P), biết khoảng cách từ M đến tiêu điểm bằng 6.
III. Cách vẽ đường Parabol
Hoạt động 3. Vẽ parabol (P): $y^{2} = 4x.$
Luyện tập 2. Vẽ parabol $y^{2}$ = 2px biết tiêu điểm của parabol là $F(\frac{1}{4};0)$F14;0.">.
Bài tập
Bài tập 1. Viết phương trình chính tắc của parabol trong mỗi trường hợp sau:
a) Tiêu điểm là F2(5; 0);
b) Phương trình đường chuẩn là x = –4;
c) Parabol đi qua điểm A(4; 9).
Bài tập 2. Trong mặt phẳng tọa độ Oxy, cho parabol có phương trình chính tắc y$^{2}$ = 8x.
a) Xác định tọa độ tiêu điểm và phương trình đường chuẩn của parabol.
b) Vẽ parabol.
Bài tập 3. Các vật liệu xây dựng đều có hệ số dãn nở. Vì thế, khi đặt dầm cầu, người ta thường đặt cố định một đầu dầm, đầu còn lại đặt trên một con lăn có thể di động được nhằm giải quyết sự dãn nở của vật liệu. Hình 21 minh hoạ một dầm cầu được đặt ở hai bờ kênh, giới hạn bởi hai cung parabol có cùng trục đối xúmg. Người ta thiết kế các thanh giằng nối hai cung parabol đó sao cho các thanh giằng theo phương thẳng đứng cách đều nhau và cách đều hai đầu dầm.
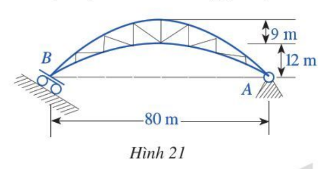
Tính tổng độ dài của các thanh giằng theo phương thẳng đứng.





