II. Tam giác PascalHoạt động 2.Ta đã biết:$(a+b)^{2}=C_{2}^{...
Câu hỏi:
II. Tam giác Pascal
Hoạt động 2.
Ta đã biết:
$(a+b)^{2}=C_{2}^{0}a^{2}+C_{2}^{1}ab+C_{2}^{2}b^{2}$
$(a+b)^{3}=C_{3}^{0}a^{3}+C_{3}^{1}a^{2}b+C_{3}^{2}ab^{2}+C_{3}^{3}b^{3}$
$(a+b)^{4}=C_{4}^{0}a^{4}+C_{4}^{1}a^{3}b+C_{4}^{2}a^{2}b^{2}+C_{4}^{3}ab^{3}+C_{4}^{4}b^{4}$
$(a+b)^{5}=C_{5}^{0}a^{5}+C_{5}^{1}a^{4}b+C_{5}^{2}a^{3}b^{2}+C_{5}^{3}a^{2}b^{3}+C_{5}^{4}ab^{4}+C_{5}^{5}b^{5}$
Ta sắp xểp những hệ số tổ hợp ở trên như sau:
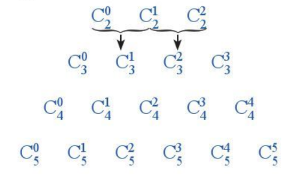
Nêu phép toán để từ hai số hạng của dòng trên suy ra được số hạng tương ứng (thể hiện ở mũi tên ↓) ở dòng dưới trong bảng các hệ số nói trên.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Phương
Phương pháp giải:
Để từ hai số hạng của dòng trên suy ra số hạng tương ứng ở dòng dưới, ta có thể áp dụng công thức tổ hợp như sau:
$(a+b)^{n+1}$ có thể được phân tích thành tổ hợp của $(a+b)^n$ và $(a+b)$.
Ví dụ, xét trường hợp $(a+b)^4$:
$(a+b)^{4} = (a+b)\cdot(a+b)^3$
Ta sẽ có:
$(a+b)^{4} = (a+b)(C_{3}^{0}a^3 + C_{3}^{1}a^2b + C_{3}^{2}ab^2 + C_{3}^{3}b^3)$
Mở rộng biểu thức, ta có:
$(a+b)^{4} = C_{3}^{0}a^4 + C_{3}^{1}a^3b + C_{3}^{2}a^2b^2 + C_{3}^{3}ab^3 + (C_{3}^{0}a^3b + C_{3}^{1}a^2b^2 + C_{3}^{2}ab^3 + C_{3}^{3}b^4)$
Như vậy, chúng ta đã tìm ra cách để phân chia các hệ số tổ hợp ở dòng trên để suy ra hệ số tổ hợp tương ứng ở dòng dưới.
Câu trả lời cho câu hỏi:
Để từ hai số hạng của dòng trên suy ra được số hạng tương ứng ở dòng dưới trong bảng các hệ số tổ hợp nói trên, ta tiến hành áp dụng công thức tổ hợp như đã mô tả ở phương pháp giải ở trên. Do đó, phép toán cần thực hiện để từ hai số hạng của dòng trên suy ra số hạng tương ứng ở dòng dưới là phép cộng các hệ số tổ hợp ở cùng một vị trí trong biểu thức mở rộng.
Để từ hai số hạng của dòng trên suy ra số hạng tương ứng ở dòng dưới, ta có thể áp dụng công thức tổ hợp như sau:
$(a+b)^{n+1}$ có thể được phân tích thành tổ hợp của $(a+b)^n$ và $(a+b)$.
Ví dụ, xét trường hợp $(a+b)^4$:
$(a+b)^{4} = (a+b)\cdot(a+b)^3$
Ta sẽ có:
$(a+b)^{4} = (a+b)(C_{3}^{0}a^3 + C_{3}^{1}a^2b + C_{3}^{2}ab^2 + C_{3}^{3}b^3)$
Mở rộng biểu thức, ta có:
$(a+b)^{4} = C_{3}^{0}a^4 + C_{3}^{1}a^3b + C_{3}^{2}a^2b^2 + C_{3}^{3}ab^3 + (C_{3}^{0}a^3b + C_{3}^{1}a^2b^2 + C_{3}^{2}ab^3 + C_{3}^{3}b^4)$
Như vậy, chúng ta đã tìm ra cách để phân chia các hệ số tổ hợp ở dòng trên để suy ra hệ số tổ hợp tương ứng ở dòng dưới.
Câu trả lời cho câu hỏi:
Để từ hai số hạng của dòng trên suy ra được số hạng tương ứng ở dòng dưới trong bảng các hệ số tổ hợp nói trên, ta tiến hành áp dụng công thức tổ hợp như đã mô tả ở phương pháp giải ở trên. Do đó, phép toán cần thực hiện để từ hai số hạng của dòng trên suy ra số hạng tương ứng ở dòng dưới là phép cộng các hệ số tổ hợp ở cùng một vị trí trong biểu thức mở rộng.
Câu hỏi liên quan:
- I. Công thức nhị thức NewtonHoạt động 1.a) Chọn số thích hợp cho ? trong khai triển biểu thức...
- Luyện tập 1.Khai triển biểu thức $(x + 2)^{7}$.
- Luyện tập 2.Cho n ∈ ℕ*. Chứng minh $C_{n}^{...
- Luyện tập 3.Sử dụng tam giác Pascal để khai triển:a) $(x + y)^{7}$;b) $(x – 2)^{7}$.
- III. Hệ số trong khai triển nhị thức Newton1. Sự biến thiên của dãy hệ số trong khai triển nhị thức...
- Luyện tập 4.Tìm hệ số lớn nhất trong khai triển của:a) (a + b)$^{2022}$;b) (a + b)$^{2023}$.
- 2. Hệ số của x$^{k}$trong khai triển (ax+b)$^{n}$thành đa thứcHoạt động 4.Quan...
- Luyện tập 5.Xét khai triển của (x + 5)4^{15}$.a) Nêu số hạng chứa x$^{7}$, từ đó nêu hệ số...
- Bài tậpBài tập 1.Khai triển các biểu thức sau:a) (2x + y)$^{6}$;b) (x – 3y)$^{6}$;c) (x –...
- Bài tập 2.Tínha) $S= C_{2022}^{0}9^{2022}+C_{2022}^{1}9^{2021}+...+C_{2022}^{k}9^{2...
- Bài tập 3.Chứng minh:$C_{n}^{...
- Bài tập 4.Xác định hệ số của:a) x$^{12}$trong khai triển của (x + 4)$^{30}$;b) x$^{1...
- Bài tập 5.Xét khai triển của $(x+\frac{5}{2})^{12}$a) Xác định hệ số của x$^{7}$.b) Nêu số...
- Bài tập 6.Xét khai triển của $(\frac{x}{2}+\frac{1}{5})^{21}$a) Xác định hệ số của x1$^{1...
- Bài tập 7.Tìm hệ số lớn nhất trong khai triển của:a) (a + b)$^{8}$;b) (a + b)$^{9}$.
- Bài tập 8.Chứng minh công thức nhị thức Newton bằng phương pháp quy nạp:$(a+b)^{n}=C_{n}^{...
- Bài tập 9.Bằng phương pháp quy nạp, chứng minh:a) $n^{5}$– n chia hết cho 5 ∀n...
- Bài tập 10.Cho tập hợp A = {x1; x2; x3; ... ; xn} có n phần tử. Tính số tập hợp con của A.
- Bài tập 11.Một nhóm gồm 10 học sinh tham gia chiến dịch Mùa hè xanh. Nhà trường muốn chọn ra...
- Bài tập 12.Để tham gia một cuộc thi làm bánh, bạn Tiến làm 12 chiếc bánh có màu khác nhau và...
- Bài tập 13.Bác Thành muốn mua quà cho con nhân dịp sinh nhật nên đã đến một cửa hàng đồ chơi....
- Bài tập 14.Giả sử tính trạng ở một loài cây được quy định do tác động cộng gộp của n cặp alen...
Bình luận (0)





