Giải bài tập chuyên đề toán lớp 10 cánh diều bài 1 Phương pháp quy nạp toán học

Câu hỏi: Chia hình vuông cạnh 1 thành bốn hình vuông nhỏ bằng nhau, lấy ra hình vuông nhỏ thứ nhất (ở góc dưới bên trái, màu đỏ), cạnh của hình vuông đó bằng $\frac{1}{2}$.

Chia hình vuông nhỏ ở góc trên bên phải thành bốn hình vuông bằng nhau, lấy ra hình vuông nhỏ thứ hai (màu đỏ), cạnh của hình vuông đó bằng $\frac{1}{4}$

Tiếp tục quá trình trên ta được dãy các hình vuông nhỏ (màu đỏ) ở Hình 1.

Cạnh của hình vuông nhỏ thứ n (màu đỏ) bằng bao nhiêu? Vì sao?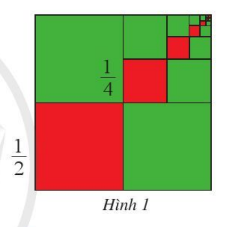

I. Phương pháp quy nạp toán học

Hoạt động: Xét mệnh đề chứa biến P(n) : "1 + 3 + 5 + ... + (2n – 1) = n$^{2}$" với n là số nguyên dương.

a) Chứng tỏ rằng P(1) là mệnh đề đúng.

b) Với k là một số nguyên dương tuỳ ý mà P(k) là mệnh đề đúng, cho biết 1 + 3 + 5 + ... + (2k – 1) bằng bao nhiêu.

c) Với k là một số nguyên dương tuỳ ý mà P(k) là mệnh đề đúng, chứng tỏ rằng P(k+1) cũng là mệnh đề đúng bằng cách chỉ ra $k^{2} + [2(k + 1) – 1] = (k+1)^{2}$.

Luyện tập 1. Chứng minh rằng với mọi n ∈ ℕ* ta có

$a) \frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+...+\frac{1}{\sqrt{n}+\sqrt{n+1}}=\sqrt{n+1}-1$

$b)\frac{2^{3}-1}{2^{3}+1}\times\frac{3^{3}-1}{3^{3}+1}\times\frac{4^{3}-1}{4^{3}+1}...\frac{n^{3}-1}{n^{3}+1}=\frac{2(n^{2}+n+1}{3n(n+1)}$

II. Áp dụng

Luyện tập 2. Chứng minh với mọi n ∈ ℕ*, $(1+\sqrt{2})^{n},(1-\sqrt{2})^{n}$ lần lượt viết được ở dạng $a_{n}+b_{n}\sqrt{2}, a_{n}-b_{n}\sqrt{2}$ , trong đó an, bn là các số nguyên dương.

Luyện tập 3. Chứng minh $16^{n} – 15n – 1$ chia hết cho 225 với mọi n ∈ ℕ*.

Bài tập

Bài tập 1. Cho $Sn = 1 + 2 + 2^{2} +... + 2^{n}$ và $Tn = 2^{n+1} – 1$, với n ∈ ℕ*.

a) So sánh S1 và T1; S2 và T2; S3 và T3.

b) Dự đoán công thức tính Sn và chứng minh bằng phương pháp quy nạp toán học

Bài tập 2. Cho $Sn=1+\frac{1}{2}+\frac{1}{2^{2}}+...+\frac{1}{2^{n}}$ và $Tn=2-\frac{1}{2^{n}}$ với n ∈ ℕ*.

a) So sánh S1 và T1; S2 và T2; S3 và T3.

b) Dự đoán công thức tính Sn và chứng minh bằng phương pháp quy nạp toán học.

Bài tập 3. Cho $Sn=\frac{1}{1\times 5}+\frac{1}{5\times 9}+\frac{1}{9\times 13}+...+\frac{1}{(4n-3)(4n+1)}$, với n ∈ ℕ*.

a) Tính S1, S2, S3, S4.

b) Dự đoán công thức tính Sn và chứng minh bằng phương pháp quy nạp toán học.

Bài tập 4. Cho q là số thực khác 1. Chứng minh: $1 + q + q^{2} +... + q^{n-1}=\frac{1-q^{n}}{1-q}$ với n ∈ ℕ*.

Bài tập 5. Chứng minh với mọi n ∈ ℕ*, ta có:

a) $4^{n} + 15n – 1$ chia hết cho 9;

b) $13^{n} – 1$ chia hết cho 6.

Bài tập 6. Chứng minh $n^{n} > (n + 1)^{n – 1}$ với n ∈ ℕ*, n ≥ 2.

Bài tập 7. Chứng minh $a^{n} – b^{n} = (a – b)(a^{n – 1} + a^{n – 2}b + ... + ab^{n –2} + b^{n – 1})$ với n ∈ ℕ*.

Bài tập 8. Cho tam giác đều màu xanh (Hình thứ nhất).

a) Nêu quy luật chọn tam giác đều màu trắng ở Hình thứ hai.

b) Nêu quy luật chọn các tam giác đều màu trắng ở Hình thứ ba.

c) Nêu quy luật tiếp tục chọn các tam giác đều màu trắng từ Hình thứ tư và các tam giác đều màu trắng ở những hình sau đó.

d) Tinh số tam giác đều màu xanh lần lượt trong các Hình thứ nhất, Hình thú hai, Hình thứ ba.

e) Dự đoán số tam giác đều màu xanh trong Hình thứ n. Chứng minh kết quả đó bằng phương pháp quy nạp toán học.

Bài tập 9. Quan sát hình 6.

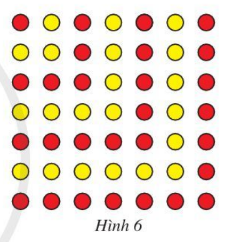
a) Nêu quy luật sắp xếp các chấm đỏ và vàng xen kẽ nhau khi xếp các chấm đó từ góc trên bên trái xuống góc dưới bên phải (tạo thành hình vuông).

b) Giả sử hình vuông thứ n có mỗi cạnh chứa n chấm. Tinh tổng số chấm được xếp trong hình vuông (kể cả trên cạnh). Chứng minh kết quả đó bằng phương pháp quy nạp toán học.

Bài tập 10. Giả sử năm đầu tiên, cô Hạnh gửi vào ngân hàng A (đồng) với lãi suất r%/năm. Hết năm đầu tiên, cô Hạnh không rút tiền ra và gửi thêm A (đồng) nữa. Hết năm thứ hai, cô Hạnh cũng không rút tiền ra và lại gửi thêm A (đồng) nữa. Cứ tiếp tục như vậy cho những năm sau. Chứng minh số tiền cả vốn lẫn lãi mà cô Hạnh có được sau n (năm) là $Tn=\frac{A(100+r)}{r}[(1+\frac{r}{100})^{n}-1]$ (đồng), nếu trong khoảng thời gian này lãi suất không thay đổi.

Bài tập 11. Một người gửi số tiền A (đồng) vào ngân hàng. Biểu lãi suất của ngân hàng như sau: Chia mỗi năm thành m kì hạn và lãi suất r%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thi cứ sau mỗi kì hạn, số tiển lãi sẽ được nhập vào vốn ban đầu. Chứng minh số tiền nhận được (bao gồm cả vốn lẫn lãi) sau n (năm) gửi là $Sn=A(1+\frac{r}{100m})^{m\times n}$ (đồng), nếu trong khoảng thời gian này người gửi không rút tiền ra và lãi suất không thay đổi.