Giải bài tập chuyên đề toán lớp 10 cánh diều bài 2 Hypebol

I. Tính đối xứng của Hypebol

Hoạt động 1. Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có phương trình chính tắc là $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$, trong đó a > 0, b > 0 (Hình 13).

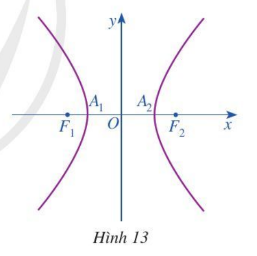
a) Tìm toạ độ hai tiêu điểm F1, F2 của hypebol (H).

b) Hypebol (H) cắt trục Ox tại các điểm A1, A2. Tìm độ dài các đoạn thẳng OA1 và OA2.

Hoạt động 2. Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có phương trình chính tắc là $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ trong đó a > 0, b > 0 (Hình 14).

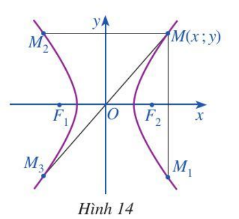
Cho điểm M(x; y) nằm trên hypebol (H). Gọi M1, M2, M3 lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc O. Các điểm M1, M2, M3 có nằm trên hypebol (H) hay không? Tại sao?

II. Hình chữ nhật cơ sở

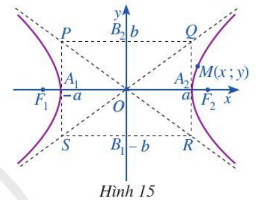
Hoạt động 3.

a) Quan sát điểm M (x; y) nằm trên hypebol (H) (Hình 15) và chứng tỏ rằng x ≤ –a hoặc x ≥ a.

b) Viết phương trình hai đường thẳng PR và QS.

Luyện tập 1. Viết phương trình chính tắc của hypebol có một đỉnh là A2(5; 0) và một đường tiệm cận là y = –3x.

III. Tâm sai của Hypebol

Hoạt động 4. Nêu định nghĩa tâm sai của elip có phương trình chính tắc là $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ với a > b > 0.

Luyện tập 2. Viết phương trình chính tắc của hypebol, biết độ dài trục ảo bằng 6 và tâm sai bằng $\frac{5}{4}$

IV. Bán kính qua tiêu cửa một điểm thuộc Hypebol

Hoạt động 5. Trong mặt phẳng, xét đường hypebol (H) là tập hợp các điểm M sao cho |MF1 – MF2| = 2a, ở đó F1F2 = 2c với c > a > 0. Ta chọn hệ trục toạ độ Oxy có gốc là trung điểm của đoạn thẳng F1F2. Trục Oy là đường trung trực của F1F2 và F2 nằm trên tia Ox (Hình 16). Khi đó F1(c; 0), F2(c; 0) là các tiêu điểm của (H).

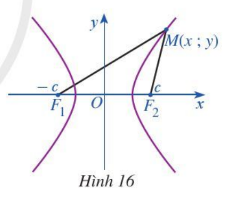
Với mỗi điểm M(x; y) thuộc đường hypebol (H), chứng minh:

a) $MF1^{2} = x^{2} + 2cx + c^{2} + y^{2}$;

b) $MF2^{2} = x^{2} – 2cx + c^{2} + y^{2}$;

c) $MF1^{2} – MF2^{2} = 4cx.$

Hoạt động 6. Với mỗi điểm M thuộc hypebol (H), từ hai đẳng thức $MF1^{2} – MF2^{2} = 4cx$ và |MF1 – MF2| = 2a, chứng minh:

$MF1=|a+\frac{c}{a}x|=|a+ex|; MF2=|a-\frac{c}{a}x|=|a-ex|$

Luyện tập 3. Cho hypebol có phương trình chính tắc $\frac{x^{2}}{144}-\frac{y^{2}}{25}=1$ Giả sử M là điểm thuộc hypebol có hoành độ là 15. Tìm độ dài các bán kính qua tiêu của điểm M.

V. Đường chuẩn của Hypebol

Hoạt động 7. Cho hypebol (H) có phương trình chính tắc $\frac{x^{2}}{a^{2}}-\frac{b^{2}}{y^{2}}=1$ với a > 0, b > 0. Xét đường thẳng $\Delta 1: x=-\frac{a}{e}$

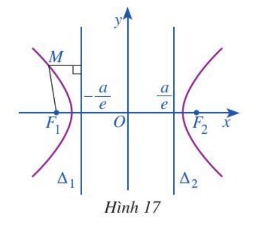
Với mỗi điểm M (x0; y0) ∈ (H) (Hình 17), tính:

a) Khoảng cách d (M, Δ1) từ điểm M(x0; y0) đến đường thẳng Δ1.

b) Tỉ số $\frac{MF1}{d(M,\Delta 1}$

Luyện tập 4. Tìm các tiêu điểm và đường chuẩn của hypebol có phương trình chính tắc là $\frac{x^{2}}{11}-\frac{y^{2}}{25}=1$

VI. Cách vẽ đường Hypebol

Hoạt động 8. Vẽ hypebol (H): $\frac{x^{2}}{9}-\frac{y^{2}}{16}=1$

Luyện tập 5. Cho hypebol (H) có một đỉnh là A1(–4; 0) và tiêu cự là 10. Viết phương trình chính tắc và vẽ hypebol (H).

Bài tập

Bài tập 1. Viết phương trình chính tắc của hypebol, biết:

a) Tiêu điểm là F1(– 3; 0) và đỉnh là A2 (2; 0).

b) Đỉnh là A2(4; 0) và tiêu cự bằng 10.

c) Tiêu điểm F2 (4; 0) và phương trình một đường tiệm cận là $y=-\frac{\sqrt{7}}{3}x$

Bài tập 2. Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc $\frac{x^{2}}{4}-\frac{y^{2}}{1}=1$

a) Xác định toạ độ các đỉnh, tiêu điểm, tiêu cự, độ dài trục thực của hypebol.

b) Xác định phương trình các đường tiệm cận của hypebol và vẽ hypebol trên.

Bài tập 3. Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc là $x^{2} – y^{2} = 1$. Chứng minh rằng hai đường tiệm cận của hypebol vuông góc với nhau.

Bài tập 4. Trong mặt phẳng tọa độ Oxy, cho hypebol $(H): \frac{x^{2}}{64}-\frac{y^{2}}{36}=1$. Lập phương trình chính tắc của elip (E), biết rằng (E) có các tiêu điểm là các tiêu điểm của (H) và các đỉnh của hình chữ nhật cơ sở của (H) đều nằm trên (E).

Bài tập 5. Dọc theo bờ biển, người ta thiết lập hệ thống định vị vô tuyến dẫn đường tầm xa để truyền tín hiệu cho máy bay hoặc tàu thuỷ hoạt động trên biển. Trong hệ thống đó có hai đài vô tuyến đặt lần lượt tại địa điểm A và địa điểm B, khoảng cách AB = 650 km (Hình 18). Giả sử có một con tàu chuyển động trên biển với quỹ đạo là hypebol nhận A và B là hai tiêu điểm.

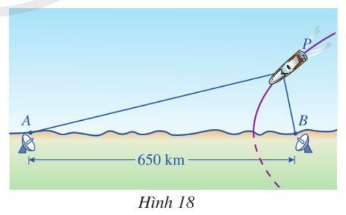
Khi đang ở vị trí P, máy thu tín hiệu trên con tàu chuyển đổi chênh lệch thời gian nhận các tín hiệu từ A và B thành hiệu khoảng cách |PA – PB|. Giả sử thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A là 0,0012 s. Vận tốc di chuyển của tín hiệu là $3 \times  108$ m/s.

a) Lập phương trình hypebol mô tả quỹ đạo chuyển động của con tàu.

b) Chứng tỏ rằng tại mọi thời điểm trên quỹ đạo chuyển động thì thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A luôn là 0,0012 s.