Bài tập5.13. Cho hai biểu đồ chấm điểm biểu diễn hai mẫu số liệu A, B như sau:trong đó, mỗi...
Câu hỏi:
Bài tập 5.13. Cho hai biểu đồ chấm điểm biểu diễn hai mẫu số liệu A, B như sau:
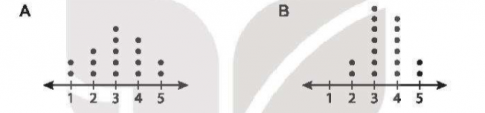
trong đó, mỗi chấm biểu diễn một giá trị trong mẫu số liệu.
Không tính, hãy cho biết:
a) Độ lệch chuẩn của mẫu số liệu nào lớn hơn.
b) Khoảng biến thiên của hai mẫu số liệu có như nhau không.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Linh
Để giải bài toán trên, ta cần tính độ lệch chuẩn của cả hai mẫu số liệu và so sánh chúng. Để tính độ lệch chuẩn của một mẫu số liệu, ta thực hiện các bước sau:1. Tính giá trị trung bình của mẫu số liệu.2. Tính độ chênh lệch của mỗi giá trị trong mẫu số liệu so với giá trị trung bình, sau đó bình phương chúng.3. Tính trung bình cộng của các bình phương đó.4. Lấy căn bậc hai của trung bình cộng đó, ta được độ lệch chuẩn của mẫu số liệu.Sau khi tính được độ lệch chuẩn của cả hai mẫu số liệu, ta so sánh chúng để xác định mẫu nào có độ lệch chuẩn lớn hơn.Về phần b, để so sánh khoảng biến thiên của hai mẫu số liệu, ta cần tìm giá trị nhỏ nhất và lớn nhất trong mỗi mẫu số liệu, sau đó tính khoảng cách giữa chúng. Nếu khoảng cách giữa giá trị nhỏ nhất và lớn nhất của hai mẫu số liệu không giống nhau, tức là hai mẫu số liệu có khoảng biến thiên khác nhau.Với câu trả lời trên, bạn có thể viết lại một cách chi tiết hơn và đầy đủ hơn bằng cách mô tả cụ thể cách tính độ lệch chuẩn của mỗi mẫu số liệu và cách tính khoảng biến thiên của họ.
Câu hỏi liên quan:
- Bài tập 5.14. Cho hai dãy số liệu sau:A: 4 5 7 ...
- Bài tập 5.15. Điểm số của hai vận động viên bắn cung trong 10 lần bắn thử để chuẩn bị cho Olympic...
- Bài tập 5.16. Trong các dãy số liệu sau, dãy nào có độ lệch chuẩn lớn nhát?(a) 98 99 100 101 1...
- Bài tập 5.17. Mẫu số liệu sau là chiều cao (đơn vị: cm) của các bạn trong tổ của Lan:165 168 157...
- Bài tập 5.18.Bình dùng đồng hồ đo thời gian để một vật rơi tự do (đơn vị: giây) từ vị trí A...
Bình luận (0)





