Giải bài tập sách bài tập (SBT) toán lớp 7 kết nối tri thức Bài tập ôn tập cuối năm
Hướng dẫn giải Bài tập ôn tập cuối năm trang 69 sách bài tập toán lớp 7
Trong vở bài tập này, chúng ta sẽ cùng tìm hiểu cách giải các bài tập ôn tập cuối năm trang 69 trong sách bài tập toán lớp 7. Đây là phần rất quan trọng để học sinh ôn tập và nắm vững kiến thức đã học. Với cách hướng dẫn chi tiết và giải thích rõ ràng, hy vọng rằng mọi học sinh sẽ hiểu bài học một cách dễ dàng hơn.
Với bộ sách "Kết nối tri thức" được biên soạn theo chương trình đổi mới của Bộ giáo dục, chúng ta có cơ hội tiếp cận với những kiến thức mới và thú vị. Bài tập ôn tập cuối năm không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện kỹ năng giải quyết vấn đề và tư duy logic.
Đừng ngần ngại khi gặp khó khăn trong việc giải bài tập, hãy tự tin thử sức và luôn nhớ rằng sự cố gắng sẽ được đền đáp. Hãy cùng nhau học tập và phấn đấu để trở thành những học sinh giỏi trong môn toán!
Bài tập và hướng dẫn giải
1. Sắp xếp các số hữu tỉ sau theo thứ tự từ bé đến lớn rồi biểu diễn chúng trên trục số: $−1,5;−\frac{3}{4};1,25;1,25$
2. Tính giá trị biểu thức sau:
$B=\frac{8^{5}+(-2)^{12}}{2^{15}+64^{3}}$
3. Bạn Minh đọc một cuốn sách trong ba ngày thì xong. Ngày thứ nhất, Minh đọc được $\frac{1}{4}$ số trang sách. Ngày thứ hai, Minh đọc được $\frac{3}{5}$ số trang sách còn lại. Ngày thứ ba, Minh đọc nốt 36 trang còn lại. Hỏi cuốn sách bạn Minh có bao nhiêu trang?
4.
a)Không dùng máy tính, hãy tính $\sqrt{\frac{50}{8}}$
b)Trong hai số 1,7(3) và $\sqrt{3}$, số nào lớn hơn?
HD:Trước hết hãy dùng máy tính để tính $\sqrt{3}$.
5.
a)Trên trục số, hãy xác định điểm biểu diễn số $\sqrt{2}-1$.
b)Viết biểu thức $|1-\sqrt{2}|$ dưới dạng không chứa dấu giá trị tuyệt đối.
6. Trong một đợt phát động làm kế hoạch nhỏ, ba lớp 7A, 7B, 7C tham gia thu gom giấy vụn. Số kilogam giấy vụn gom được của ba lớp này lần lượt tỉ lệ với 2; 4; 5. Biết rằng khối lượng giấy vụn gom được của cả hai lớp 7A và 7C nhiều hơn của lớp 7B là 27 kg. Hỏi mỗi lớp thu gom được bao nhiêu kilogam giấy vụn?
7. Xe ô tô và xe máy cùng đi từ tỉnh A đến tỉnh B trên cùng một con đường. Biết rằng xe ô tô đi với vận tốc 80 km/h, xe máy đi với vận tốc 60 km/h. Thời gian đi từ A đến B của xe ô tô ít hơn thời gian đi tương ứng của xe máy là 30 phút. Hãy tính thời gian mỗi xe đi từ A đến B và độ dài quãng đường AB.
8. Hai đa thức A(x) và B(x) thoả mãn:
$A(x)+B(x)=x^{3}-5x^{2}-2x+4$ và $A(x)-B(x)=-x^{3}+3x^{2}-2$
a)Tìm A(x), B(x) rồi xác định bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức đó.
b)Tìm giá trị của mỗi đa thức A(x) và B(x) tại x = -1.
9. Cho đa thức $F(x)=x^{4}-x^{3}-6x^{2}+15x-9$
a)Kiểm tra lại rằng x = 1 và x = -3 là hai nghiệm của F(x).
b)Tìm đa thức G(x) sao cho $F(x)=(x-1)(x-3)\times G(x)$
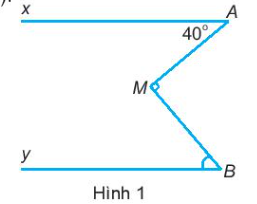
10. Tìm góc MBy trong hình 1, biết rằng Ax // By
HD: Kẻ thêm đường thẳng đi qua M và song song với Ax.
11. Cho 5 điểm A, B, C, D, E cùng nằm trên một đường thẳng d sao cho AB = DE, BC = CD. Điểm M không thuộc d sao cho MC vuông góc với d. Chứng minh rằng:
a) $\Delta MBC=\Delta MDC$ và $\Delta MAC=\Delta MEC$
b) $\Delta MAB=\Delta MED$
12. Cho tam giác ABC vuông tại đỉnh A; ba điểm M, N, P lần lượt nằm trên các cạnh BC, CA, AB của tam giác ABC sao cho M là trung điểm của BC, MN vuông góc với AC và MP vuông góc với AB. Chứng minh rằng:
a) $\Delta MNC=\Delta BPM$
b) $\widehat{NMP}=90^{\circ}$
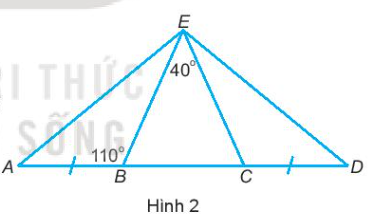
13. Cho bốn điểm A, B, C và D như Hình 2. Biết rằng $\widehat{BEC}=40^{\circ},\widehat{EBA}=110^{\circ}$ và AB = DC Chứng minh rằng:
a) Tam giác BEC cân tại đỉnh E.
b) EA = ED.
14. Tròn đưa cho Vuông một tờ giấy, trên đó có vẽ điểm C và hai đường thẳng a và b không đi qua C, cho biết hai đường thẳng a và b không song song với nhau (giao điểm của a và b nằm ngoài tờ giấy). Tròn đố Vuông vẽ được đường thẳng c đi qua C sao cho ba đường thẳng a, b, c đồng quy. Sau một hồi suy nghĩ, Vuông làm như sau (H.3):
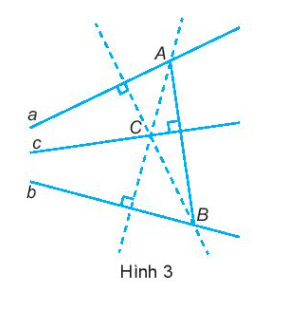
-Vẽ đường thẳng đi qua C và vuông góc với a. Đường thẳng này cắt b tại B.
-Vẽ đường thẳng đi qua C và vuông góc với b. Đường thẳng này cắt a tại A.
Vuông khẳng định rằng đường thẳng c cần vẽ chính là đường thằng đi qua C và vuông góc với AB.
Em hãy giải thích tại sao Vuông lại khẳng định như vậy.
15.
a) Chứng minh rằng nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại đỉnh A.
b) Cho đoạn thẳng AB. Hãy nêu một cách sử dụng kết quả của câu a để vẽ đường thẳng vuông góc với AB tại A (bằng thước vàpa)
16. Cho hai biểu đồ sau biểu diễn các số liệu tại một trường Trung học cơ sở:
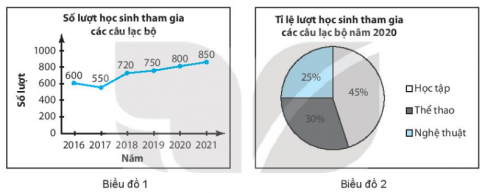
a) Biểu đồ a biểu diễn đại lượng nào theo thời gian?
b) Nêu nhận xét về sự thay đổi số lượt học sinh tham gia các câu lạc bộ từ năm 2016 đến năm 2021.
c) Lập bảng thống kê cho số liệu biểu diễn trong Biểu đồ 2.
d) Tính số lượt học sinh đăng kí trong mỗi câu lạc bộ trong năm 2020.
17. Một nhà mạng muốn tìm hiểu loại nhạc chuông của điện thoại di động được người dùng yêu thích, đã lập phiếu khảo sát như hình bên và dự kiến tiến hành thu nhập dữ liệu theo 2 cách sau:
Cách 1: Phát phiếu điều tra cho 100 người tham dự một buổi hoà nhạc thính phòng.
Cách 2: Gửi phiếu điều tra đến 100 người dùng được lựa chọn một cách ngẫu nhiên.
a) Dữ liệu thu được thuộc loại nào?
b)Theo em, dữ liệu thu được trong mỗi cách trên có đại diện cho toàn bộ người dùng dịch vụ của nhà mạng không?

18. Cho một hộp đựng n viên bi màu xanh và m viên bi màu đỏ. Lấy ngẫu nhiên một viên bi trong hộp.
a)Tìm điều kiện của m và n để biến cố “Lấy được viên bi màu đỏ” có:
- Xác xuất bằng 1;
- Xác định bằng 0;
- Xác xuất bằng $\frac{1}{2}$.
b)* Giả sử n = 10; m = 5. Tính xác suất để lấy được viên bi màu đỏ.





