7.35.Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hình elip, chiều...
Câu hỏi:
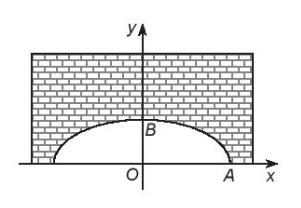
7.35. Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hình elip, chiều rộng của hầm là 12 m, khoảng cách từ điểm cao nhất của elip so với mặt đường là 3 m. Người kĩ sư này muốn đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Biết rằng những loại xe tải có chiều cao 2,8 m thì có chiều rộng không quá 3 m. Hỏi chiếc xe tải có chiều cao 2,8 m có thể đi qua hầm được không?
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Long
Để giải bài toán, ta cần tìm phương trình của hình elip mô tả mặt cắt của đường hầm. Khi đó, ta có phương trình chính tắc của elip: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$, trong đó $a$ và $b$ lần lượt là bán kính lớn và bán kính nhỏ của elip.Với các điểm trên elip là $A(6, 0)$ và $B(0, 3)$, ta thay vào phương trình elip và giải hệ phương trình để tìm $a$ và $b$. Ta được $a = 6$ và $b = 3$, suy ra phương trình elip là $\frac{x^{2}}{36} + \frac{y^{2}}{9} = 1$.Với chiều cao của xe tải là 2.8 m và chiều rộng không quá 3 m, khi xe tải di chuyển chính giữa hầm, ta sẽ xét điểm trên elip với $x = 1.5$ (vì chiều rộng của xe là 3 m ta lấy phân nửa). Tính toán ta được $y \approx 2.905 > 2.8$.Như vậy, chiếc xe tải có chiều cao 2.8 m có thể đi qua hầm một chiều được, tuy nhiên cần lưu ý phải đi vào chính giữa hầm.Vậy câu trả lời cho câu hỏi là: "Chiếc xe tải có chiều cao 2.8 m có thể đi qua hầm được, nhưng cần chú ý đi vào chính giữa hầm để tránh va chạm".
Câu hỏi liên quan:
- BÀI TẬP7.28.Cho elip (E) có phương trình $\frac{x^{2}}{36}+\frac{y^{2}}{16}=1$. Tìm tiêu điểm...
- 7.29.Cho hypebol (H) có phương trình $\frac{x^{2}}{16}-\frac{y^{2}}{20}=1$. Tìm tiêu điểm và...
- 7.30.Cho parabol (P) có phương trình $y^{2}$= 4x. Tìm tiêu điểm và đường chuẩn của...
- 7.31.Viết phương trình chính tắc của elip (E), biết (E) đi qua điểm A(6; 0) và có tiêu cự...
- 7.32.Viết phương trình chính tắc của hypebol (H), biết (H) đi qua điểm $M(3\sqrt{2};-4)$ và...
- 7.33.Viết phương trình chính tắc của parabol (P), biết rằng (P) có đường chuẩn là đường thẳng...
- 7.34.Cho parabol (P) có phương trình là y$^{2}$= 16x. Gọi Δ là đường thẳng bất kì đi...
- 7.36.Cho điểm M(x0; y0) thuộc elip (E) có phương...
- 7.37.Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một đường elip với tâm Trái Đất là...
Bình luận (0)





