Giải bài tập sách bài tập (SBT) toán lớp 7 chân trời sáng tạo bài 2 Làm quen với xác suất của biến cố ngẫu nhiên

BÀI TẬP

Bài 1. Gieo một con xúc xắc 6 mặt cân đối. Tính xác suất của các biến cố sau.

A: "Xuất hiện mặt có 2 chấm";

B: "Xuất hiện mặt có số chấm chia hết cho 4";

C: "Xuất hiện mặt có số chấm chia hết cho 7";

D: "Xuất hiện mặt có số chấm là ước của 60";

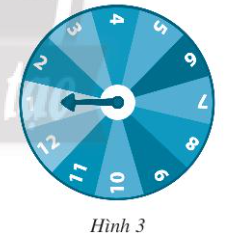
Bài 2. Trên tường có một đĩa hình tròn có cấu tạo đồng chất và cân đối (Hình 3). Mặt đĩa được chia thành 12 hình quạt bằng nhau và được đánh số từ 1 đến 12. Hoàng quay đĩa quanh trục gắn ở tâm và quan sát xem khi dừng lại mũi tên chỉ vào ô số mấy. Tính xác suất của các biến cố sau:

A: "Mũi tên chỉ vào ô số 7";

B: "Mũi tên chỉ vào ô ghi số lẻ";

C: "Mũi tên chỉ vào ô ghi số lớn hơn 11".

Bài 3. Một chiếc hộp kín có chứa 5 quả bóng có kích thước và khối lượng như nhau, và được ghi lần lượt các số 5; 10; 15; 20; 25. Lây ra ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất của các biến cố sau.

A: "Quả bóng lấy ra ghi số nguyên tố".

B: "Quả bóng lấy ra ghi số chia hết cho 5".

C: "Quả bóng lấy ra ghi số chia hết cho 3".

D: "Quả bóng lấy ra ghi số là bội của 6".

Bài 4. Một chiếc hộp kín có chứa 5 quả bóng xanh, 5 quả bóng đỏ và 5 quả bóng trắng có kích thước và khối lượng như nhau. Lấy ra ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất của biến cố bóng lấy ra có màu xanh.

Bài 5. Trong hộp có 1 viên bi xanh, 1 viên bi trắng và 1 viên bi đỏ có kích thước và trọng lượng như nhau. Lấy ra ngẫu nhiên 2 viên bi từ hộp. Tính xác suất của các biến cố sau:

A: "Hai viên bi lấy ra có cùng màu"

B: "Không có viên bi nào có màu xanh hay trắng trog 2 viên bi được chọn".

Bài 6. Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị: mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2016 - 2020. Chọn ngẫu nhiên 1 năm trong 6 năm đó. Tính xác suất của các biến cố sau:

A: "Tại năm được chọn, lượng mưa ở Cà Mau cao hơn ở Lai Châu",

B: "Tại năm được chọn, lượng mưa ở Cà Mau thấp hơn 25 m";

C: "Tại năm được chọn, lượng mưa ở Lai Châu gấp hai lần lượng mưa ở Cà Mau".

Bài 7. Gieo hai đồng xu cân đối và đồng chất. Hãy so sánh xác suất xảy ra của các biến cố sau:

A: "Có không quá hai đồng sấp";

B: "Cả hai đồng đều sấp";

C: "Có ít nhất một đồng sấp".

Bài 8. Mật khẩu mở máy tính của Cường gồm 8 kí tự, trong đó 2 kí tự đầu là chữ số, 6 kí tự sau là chữ cái. Không may Cường quên mất kí tự đầu tiên. Cường chọn ra 2 chữ số một cách ngẫu nhiên và thử mở máy tính. Tính xác suất để Cường mở được máy tính.