Bài tập 6. Một cái cầu có dây cáp treo hình parabol, cầu dài 120 m và được nâng đỡ bởi những thanh...
Câu hỏi:
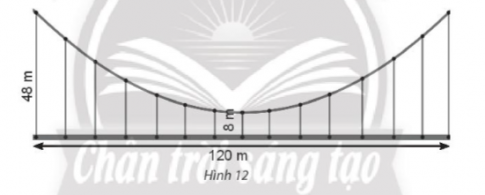
Bài tập 6. Một cái cầu có dây cáp treo hình parabol, cầu dài 120 m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 48 m, thanh ngắn nhất là 8 m (Hình 12). Tính chiều dài của thanh cách điểm giữa cầu 20 m.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Hưng
Phương pháp giải:1. Chọn hệ tọa độ sao cho parabol có phương trình $y^{2} = 2px$.2. Thay tọa độ điểm M(40; 60) vào phương trình trên để tính được $p = \frac{60^{2}}{80} = 45$.3. Thay tọa độ điểm N(x; 20) vào phương trình $y^{2} = 2 \times 45 \times x$ để tính được $x = \frac{20^{2}}{90} \approx 4,44$m.Vậy chiều dài của thanh cách điểm giữa cầu 20m là khoảng cách 12,44 m.
Câu hỏi liên quan:
- Bài tập 1. Viết phương trình chính tắc của:a) Elip có trục lớn bằng 12 và trục nhỏ bằng 8;b)...
- Bài tập 2. Viết phương trình chính tắc của các đường conic dưới đây. Gọi tên và tìm tọa độ các tiêu...
- Bài tập 3.Để cắt một bảng hiệu quảng cáo hình elip có trục lớn là 1 m và trục nhỏ là 0,6 m từ...
- Bài tập 4. Thang leo gợn sóng cho trẻ em trong công viên có hai khung thép cong hình nửa elip cao 1...
- Bài tập 5. Một tháp làm nguội của một nhà máy có mặt cắt là hình hypebol có phương trình...
Bình luận (0)





