4. Giới hạn vô cựcKhám phá 5 trang 68 toán lớp 11 tập 1 Chân trời:Dựng một dãy hình vuông...
Câu hỏi:
4. Giới hạn vô cực
Khám phá 5 trang 68 toán lớp 11 tập 1 Chân trời: Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vi (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu $u_{n}$ (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ n.
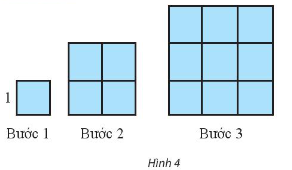
a) Với n như thế nào thì $u_{n}$ vượt quá 10000; 1000000?
b) Cho hình có diện tích S. Với n như thế nào thì $u_{n}$ vượt quá S?
Câu trả lời:
Người trả lời: GV. Đỗ Thị Hạnh
Phương pháp giải:Ta biết rằng diện tích hình vuông ở bước thứ n là $u_{n} = n^{2}$.a) Để $u_{n}$ vượt quá 10000, ta cần tìm giá trị của n sao cho $n^{2} > 10000$. Tức là $n > \sqrt{10000} = 100$. Vậy nếu $n > 100$, thì $u_{n}$ vượt quá 10000. Tương tự, để $u_{n}$ vượt quá 1000000 thì cần $n > 1000$.b) Để $u_{n}$ vượt quá diện tích S, ta cần $n^{2} > S$, tức là $n > \sqrt{S}$.Vậy câu trả lời cho câu hỏi trên là:a) Để $u_{n}$ vượt quá 10000, cần n > 100; để $u_{n}$ vượt quá 1000000, cần n > 1000.b) Để $u_{n}$ vượt quá diện tích S, cần n > √S.
Câu hỏi liên quan:
- 1. Giới hạn hữu hạn của dãy sốGiới hạn 0 của dãy sốKhám phá 1 trang 64 toán lớp 11 tập 1 Chân...
- Thực hành 1 trang 65 toán lớp 11 tập 1 Chân trời:Tìm các giới hạn sau:a)...
- Giới hạn hữu hạn của dãy sốKhám phá 2 trang 65 toán lớp 11 tập 1 Chân trời:Cho dãy số...
- Thực hành 2 trang 65 toán lớp 11 tập 1 Chân trời:Tìm các giới hạn sau:a) $lim\left ( 2+\left...
- 2. Các phép toán về giới hạn hữu hạn của dãy sốKhám phá 3 trang 66 toán lớp 11 tập 1 Chân trời: Ở...
- Thực hành 3 trang 66 toán lớp 11 tập 1 Chân trời:Tìm các giới hạn sau:a)...
- 3. Tổng của cấp số nhân lùi vô hạnKhám phá 4 trang 67 toán lớp 11 tập 1 Chân trời:Từ một hình...
- Thực hành 4 trang 68 toán lớp 11 tập 1 Chân trời:Tính tổng của cấp số nhân lùi vô hạn...
- Vận dụng 1 trang 68 toán lớp 11 tập 1 Chân trời:Từ tờ giấy, cắt một hình tròn bán kính R (cm)...
- Bài tậpBài tập 1 trang 69 toán lớp 11 tập 1 Chân trời:Tìm các giới hạn sau:a)...
- Bài tập 2 trang 69 toán lớp 11 tập 1 Chân trời:Tính tổng của các cấp số nhân lùi vô hạn...
- Bài tập 3 trang 69 toán lớp 11 tập 1 Chân trời:Viết số thập phân vô hạn tuần hoàn 0,444......
- Bài tập 4 trang 70 toán lớp 11 tập 1 Chân trời:Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị...
- Bài tập 5 trang 70 toán lớp 11 tập 1 Chân trời:Xét quá trình tạo ra hình có chu vi vô cực và...
Bình luận (0)





