3. TÂM SAIHoạt động khám phá 3: Cho biết tỉ số e=$\frac{c}{a}$của các elip lần lượt là...
Câu hỏi:
3. TÂM SAI
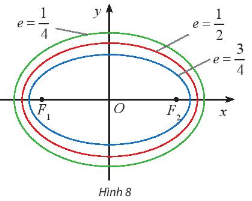
Hoạt động khám phá 3: Cho biết tỉ số e=$\frac{c}{a}$ của các elip lần lượt là $\frac{3}{4}$, $\frac{1}{2}$, $\frac{1}{4}$ (Hình 8)
Tính tỉ số $\frac{a}{b}$ theo e và nêu nhận xét về sự thay đổi của hình dạng elip gắn với hình chữ nhật cơ sở khi e thay đổi.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Long
Để giải bài toán này, ta sử dụng công thức $\frac{a}{b}=\sqrt{1-e^2}$ để tính tỉ số $\frac{a}{b}$ theo tâm sai e.Với giá trị ban đầu e = $\frac{3}{4}$, thì $\frac{a}{b}=\sqrt{1-(\frac{3}{4})^2}=\sqrt{\frac{7}{16}}=\frac{\sqrt{7}}{4}$Với giá trị e = $\frac{1}{2}$, ta có $\frac{a}{b}=\sqrt{1-(\frac{1}{2})^2}=\sqrt{\frac{3}{4}}=\frac{\sqrt{3}}{2}$Với giá trị e = $\frac{1}{4}$, ta có $\frac{a}{b}=\sqrt{1-(\frac{1}{4})^2}=\sqrt{\frac{15}{16}}=\frac{\sqrt{15}}{4}$Nhận xét: Khi tâm sai e càng bé (gần 0), tỉ số $\frac{a}{b}$ càng gần 1, elip trông càng "béo". Khi tâm sai e càng lớn (gần 1), tỉ số $\frac{a}{b}$ càng gần 0, elip trông càng "dẹt".
Câu hỏi liên quan:
- 1. TÍNH ĐỐI XỨNG CỦA ELIPHoạt động khám phá 1: Cho elip(E) có phương trình chính...
- 1. TÍNH ĐỐI XỨNG CỦA ELIPHoạt động khám phá 1: Cho elip(E) có phương trình chính...
- Thực hành 1: Viết phương trình chính tắc của elip có kích thước của hình chữ nhật cơ sở là 8 và 6....
- Vận dụng 1: Hãy gấp một mảnh giấy hình elip thành bốn phần chồng khít lên nhau.
- 2. BÁN KÍNH QUA TIÊUHoạt động khám phá:Cho điểm M(x; y) nằm trên elip...
- Thực hành 2:a, Tính độ dài hai bán kính qua tiêu của điểm M(x,y) trên elip...
- Vận dụng 2: Người ta chứng minh được rằng nếu ánh sáng hay âm thanh đi từ một tiêu điểm, khi đến...
- Thực hành 3:a,Tìm tâm sai của elip (E): $\frac{x^2}{100}$ + $\frac{y^2}{99}$ = 1 và...
- Vận dụng 3: TRong hệ mặt trời, các hành tinh chuyển động theo quỹ đạo là đường elip nhận tâm mặt...
- 4. ĐƯỜNG CHUẨNHoạt động khám phá 4:Cho điểm M(x; y) trên elip (E):$\frac{x^2}{a^2}$ +...
- Thực hành 4: Tìm tọa độ hai tiêu điểm và viết phương trình hai đường chuẩn tương ứng của các elip...
- Vận dụng 4: Lập phương trình chính tắc của elip có tiêu cự bằng 6 khoảng cách giữa hai đường chuẩn...
- BÀI TẬPBài tập 1: Cho elip (E): $\frac{x^2}{64}$ + $\frac{x^2}{36}$ = 1a, Tìm tâm sau,...
- Bài tập 2: Tìm các điểm trên elip (E): $\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1 có độ dài hai bán kính...
- Bài tập 3: Lập phương trìn chính tắc của elip có tiêu cự bằng 12 và khoảng cách giữa hai đường...
- Bài tập 4: Cho elip (E):$\frac{x^2}{9}$ + $\frac{x^2}{1}$ = 1a) Tìm tâm sai và độ dài hai bán kính...
- Bài tập 5:Trái Đất chuyển động theo một quỹ đạo là đường elip có tâm sai là 0,0167 và nhận...
- Bài tập 6:Ngày 04/10/1957, Liên Xô đã phóng thành công vệ tinh nhân tạo đầu tiên vào không...
- Thực hành 1: Viết phương trình chính tắc của hypebol có kích thước của hình chữ nhật cơ sở là 8 và...
Bình luận (0)





