Vận dụng 4:Một vật thể có quỹ đạo là một nhánh của hypebol (H), nhận tâm Mặt Trời làm tiêu...
Câu hỏi:
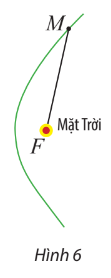
Vận dụng 4: Một vật thể có quỹ đạo là một nhánh của hypebol (H), nhận tâm Mặt Trời làm tiêu điểm (Hình 6). Cho biết tâm sai của (H) bằng 1,2 và khoảng cách gần nhất giữa vật thể và tâm Mặt Trời là 2 . $10^8$ km.
a) Lập phương trình chính tắc của (H).
b) Lập công thức tính bán kính qua tiêu của vị trí M(x; y) của vật thể trong mặt phẳng toạ độ.
Câu trả lời:
Người trả lời: GV. Đỗ Văn Linh
a) Phương pháp giải: - Chọn hệ trục toạ độ sao cho tiêu điểm F2 của (H) trùng với tâm Mặt Trời, trục Ox đi qua đỉnh và tiêu điểm này của (H), đơn vị trên các trục là km.- Gọi phương trình chính tắc của (H) là $\frac{x^2}{a^2} + \frac{y^2}{b^2}=1$ (a > 0, b > 0).- Gọi toạ độ của vật thể là M(x; y).- Áp dụng công thức bán kính qua tiêu, ta có: khoảng cách giữa vật thể và tâm Mặt Trời là = ex – a ≥ ea – a (vì vật thể nằm ở nhánh bên phải trục Ox nên x ≥ a).- Như vậy khoảng cách gần nhất giữa vật thể và tâm Mặt Trời là ea – a.b) Câu trả lời: - Phương trình chính tắc của (H) là $\frac{x^2}{(ea)^2} + \frac{y^2}{b^2} = 1$.- Bán kính qua tiêu của vị trí M(x; y) của vật thể trong mặt phẳng toạ độ là ea.
Câu hỏi liên quan:
- 1. TÍNH ĐỐI XỨNG CỦA ĐƯỜNG HYPEBOLHoạt động khám phá 1: Cho hypebol (H) với phương trình chính...
- Vận dụng 1: Khi bay với vận tốc siêu nhanh( tốc độ chuyển động lớn hơn tốc độ âm thanh trong cùng...
- 2. BÁN KÍNH QUA TIÊUHoạt động khám phá 2: Cho điểm M(x,y)nằm trên...
- Thực hành 2: Tính độ dài hai bán kính qua tiêu của điểm M(x;y) trên hypebol(H):...
- Vận dụng 2: Tính độ dài hai bán kính qua tiêu của đingr A2(a,0) trên...
- 3. TÂM SAIHoạt động khám phá 3: Cho hypebol(H): (H):$\frac{x^2}{a^2}$ -...
- Thực hành 3: Tìm tâm sai của các hypebol sau:a, (H1): $\frac{x^2}{4}$ + $\frac{y^2}{1}$=1b,...
- Vận dụng 3: Cho hypebol (H) có tâm sai bằng $\sqrt{2}$. Chứng minh trục thực và trục ảo của (H) có...
- 4. ĐƯỜNG CHUẨNHoạt động khám phá 4: Cho điểm M((x; y) trên hypebol(H):...
- Thực hành 4: Tìm tọa đọ hai tiêu điểm và viết phương trình hai đưởng chuẩn tướng ứng của các...
- Vận dụng 5:Lập phương trình chính tắc của hypebol có tiêu cự bằng 26 và khoảng cách giữa hai...
- BÀI TẬP1.Cho hypebol (H):$\frac{x^2}{144}$ + $\frac{y^2}{25}$=1a) Tìm tâm sai và độ dài...
- 2. Lập phương trình chính tắc của hypebol có tiêu cự bằng 20 và khoảng cách giữa hai đường chuẩn...
- 3.Cho đường tròn (C) tâm F1, bán kính r và một điểm F2thoả mãn F1F2= 4ra) Chứng...
- 4. Trong hoát động mở đầu bài học, cho biết khoảng cách giữa hai trạm vô tuyến là 600km, vận tốc...
Bình luận (0)





