4. ĐƯỜNG CHUẨNHoạt động khám phá 4: Cho điểm M((x; y) trên hypebol(H):...
Câu hỏi:
4. ĐƯỜNG CHUẨN
Hoạt động khám phá 4: Cho điểm M((x; y) trên hypebol
(H): $\frac{x^2}{a^2}$ + $\frac{y^2}{b^2}$=1 và hai đường thẳng
![]()
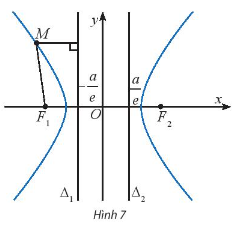
Gọi d(M; Δ1), d(M; Δ2) lần lượt là khoảng cách từ M đến các đường thẳng Δ1, Δ2.
Ta có: ![]() e
e
Dựa theo cách tính trên, tính ![]()
Câu trả lời:
Người trả lời: GV. Đỗ Văn Linh
Phương pháp giải:Bước 1: Viết lại phương trình đường thẳng Δ2 ở dạng x + 0y - a/c = 0.Bước 2: Tính khoảng cách từ điểm M(x; y) đến đường thẳng Δ2 bằng công thức đường chuẩn: |ax0 + by0 + c| / √(a^2 + b^2).Bước 3: Thay vào công thức với a = 1, b = 0, c = -a/c, x0 = x, y0 = y.Bước 4: Tính toán và rút gọn biểu thức để đưa ra câu trả lời.Câu trả lời đầy đủ và chi tiết hơn:Từ phương pháp trên, ta tính được d(M;Δ2) = |x - a/c| / √(1^2 + 0^2) = |x - a/c|.Vậy, khoảng cách từ điểm M(x; y) trên hyperbol đến đường thẳng Δ2 là |x - a/c|.
Câu hỏi liên quan:
- 1. TÍNH ĐỐI XỨNG CỦA ĐƯỜNG HYPEBOLHoạt động khám phá 1: Cho hypebol (H) với phương trình chính...
- Vận dụng 1: Khi bay với vận tốc siêu nhanh( tốc độ chuyển động lớn hơn tốc độ âm thanh trong cùng...
- 2. BÁN KÍNH QUA TIÊUHoạt động khám phá 2: Cho điểm M(x,y)nằm trên...
- Thực hành 2: Tính độ dài hai bán kính qua tiêu của điểm M(x;y) trên hypebol(H):...
- Vận dụng 2: Tính độ dài hai bán kính qua tiêu của đingr A2(a,0) trên...
- 3. TÂM SAIHoạt động khám phá 3: Cho hypebol(H): (H):$\frac{x^2}{a^2}$ -...
- Thực hành 3: Tìm tâm sai của các hypebol sau:a, (H1): $\frac{x^2}{4}$ + $\frac{y^2}{1}$=1b,...
- Vận dụng 3: Cho hypebol (H) có tâm sai bằng $\sqrt{2}$. Chứng minh trục thực và trục ảo của (H) có...
- Vận dụng 4:Một vật thể có quỹ đạo là một nhánh của hypebol (H), nhận tâm Mặt Trời làm tiêu...
- Thực hành 4: Tìm tọa đọ hai tiêu điểm và viết phương trình hai đưởng chuẩn tướng ứng của các...
- Vận dụng 5:Lập phương trình chính tắc của hypebol có tiêu cự bằng 26 và khoảng cách giữa hai...
- BÀI TẬP1.Cho hypebol (H):$\frac{x^2}{144}$ + $\frac{y^2}{25}$=1a) Tìm tâm sai và độ dài...
- 2. Lập phương trình chính tắc của hypebol có tiêu cự bằng 20 và khoảng cách giữa hai đường chuẩn...
- 3.Cho đường tròn (C) tâm F1, bán kính r và một điểm F2thoả mãn F1F2= 4ra) Chứng...
- 4. Trong hoát động mở đầu bài học, cho biết khoảng cách giữa hai trạm vô tuyến là 600km, vận tốc...
Bình luận (0)





