Giải bài tập 1 Các góc ở vị trí đặc biệt
Giải bài 1: Các góc ở vị trí đặc biệt - Sách chân trời sáng tạo toán lớp 7 tập 1
Trong bài này, chúng ta sẽ tìm hiểu về các góc ở vị trí đặc biệt như hai góc kề bù, hai góc đối đỉnh và tính chất của chúng. Hãy cùng khám phá và giải các bài tập sau đây:
1. Hai góc kề bù
Hoạt động khám phá 1:
a) Quan sát Hình 1 và cho biết hai góc $\widehat{xOy}$ và $\widehat{yOz}$ có cạnh nào chung và điểm trong nào chung.
b) Đo các góc $\widehat{xOy}$, $\widehat{yOz}$, $\widehat{xOz}$ trong Hình 1 và so sánh tổng số đo của $\widehat{xOy}$ và $\widehat{yOz}$ với $\widehat{xOz}.
c) Tính tổng số đo của hai góc $\widehat{mOn}$ và $\widehat{nOp}$ trong Hình 2.
Thực hành 1:
a) Tìm các góc kề với $\widehat{tOz}$.
b) Tìm số đo của góc kề bù với $\widehat{mOn}$.
c) Tìm số đo của $\widehat{nOy}$.
d) Tìm số đo của góc kề bù với $\widehat{tOz}$.
2. Hai góc đối đỉnh
Hoạt động khám phá 2:
Cho hai đường thẳng xy và zt cắt nhau tại O (Hình 7), hãy cho biết quan hệ về cạnh, quan hệ về đỉnh của $\widehat{O1}$ và $\widehat{O3}$.
Thực hành 2:
a) Vẽ hai đường thẳng ab và cd cắt nhau tại điểm I và xác định các cặp góc đối đỉnh trên hình vẽ.
b) Xác định cặp góc $\widehat{xDy}$ và $\widehat{zDt}$ có phải là các cặp góc đối đỉnh hay không.
3. Tính chất của hai góc đối đỉnh
Hoạt động khám phá 3:
a) Đo $\widehat{O1}$ và $\widehat{O3}$, so sánh số đo hai góc đó.
b) Đo $\widehat{O2}$ và $\widehat{O4}$, so sánh số đo hai góc đó.
Thực hành 3:
a) Tìm góc đối đỉnh của $\widehat{yOv}$.
b) Tính số đo của $\widehat{uOz}$.
Vậy là chúng ta đã tìm hiểu về các góc ở vị trí đặc biệt và tính chất của chúng thông qua các bài tập trong sách. Hy vọng rằng các em học sinh sẽ hiểu và nắm vững kiến thức để áp dụng vào bài tập thực hành một cách chính xác. Chúc các em học tốt!
Bài tập và hướng dẫn giải
Bài 1 trang 72 toán lớp 7 tập 1 CTST
Quan sát Hình 14.
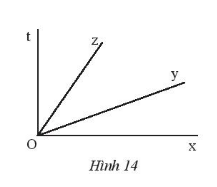
a) Tìm các góc kề với $\widehat{xOy}$
b) Tìm số đo của $\widehat{tOz}$ nếu cho biết:
$\widehat{xOy}$ = 20o ;$\widehat{xOt}$ =90∘; $\widehat{yOz}$ = $\widehat{tOz}$.
Bài 2 trang 72 toán lớp 7 tập 1 CTST
Cho hai góc $\widehat{xOy}$, $\widehat{yOz}$ kề bù với nhau. Biết $\widehat{xOy}$ =25o . Tính xOy^,yOz^" data-mce-mark="1">xOy^,yOz^" data-mce-mark="1">xOy^,yOz^" data-mce-mark="1">$\widehat{yOz}$.
Bài 3 trang 72 toán lớp 7 tập 1 CTST
Cho hai góc kề nhau $\widehat{AOB}$ và $\widehat{BOC}$ với $\widehat{AOC}$ = 80o. Biết $\widehat{AOB} =\frac{1}{5} \widehat{AOC}$. Tính số đo các góc $\widehat{AOB}$ và $\widehat{BOC}$
Bài 4 trang 72 toán lớp 7 tập 1 CTST
Tìm số đo các góc còn lại trong mỗi hình sau:
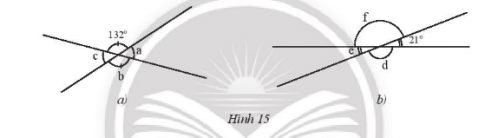
Bài 5 trang 72 toán lớp 7 tập 1 CTST
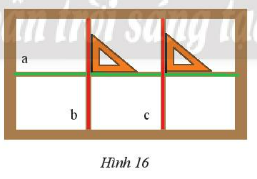
Cặp cạnh nào của cac ô cửa sổ (Hình 16) vuông góc với nhau. Hãy dùng kí hiệu ($\perp$) để biểu diễn chúng.