Giải bài tập 5 Hai dạng phương trình quy về phương trình bậc hai
Giải bài tập 5 trong sách "Hai dạng phương trình quy về phương trình bậc hai"
Trong bài này, chúng ta sẽ giải hai dạng phương trình quy về phương trình bậc hai từ sách cánh diều toán lớp 10 tập 1. Bài tập đưa ra phần đáp án chuẩn và hướng dẫn giải chi tiết từng bài tập trong chương trình học.
Bài 1: Giải phương trình: $\sqrt{3x^2-4x+1}=\sqrt{x^2+x-1}$
Hướng dẫn giải: Bình phương hai vế ta được: $3x^2-4x+1=x^2+x-1$
Đưa về dạng $2x^2-5x+2=0$, ta có các nghiệm: $x=\frac{1}{2}$ (không thỏa mãn), $x=2$ (thỏa mãn). Vậy phương trình có nghiệm là $\{2\}$.
Bài 2: Giải phương trình: $\sqrt{3x-5}=x-1$
Hướng dẫn giải: Ta có $x-1 \geq 0 \Rightarrow x \geq 1$. Bình phương hai vế ta được $3x-5=x^2-2x+1$, từ đó suy ra $-x^2+5x-6=0$ với nghiệm $x=2$ và $x=3$. Vậy phương trình có nghiệm $\{2;3\}$.
Bài tập và hướng dẫn giải
Bài tập 1. Giải các phương trình sau:
a. $\sqrt{2 x-3}=\sqrt{2 x^{2}-3 x-1}$;
b. $\sqrt{4 x^{2}-6 x-6}=\sqrt{x^{2}-6}$;
c. $\sqrt{x+9}=2 x-3$;
d. $\sqrt{-x^{2}+4 x-2}=2-x$.
Bài tập 2. Giải các phương trình sau:
a. $\sqrt{2-x}+2 x=3$.
b. $\sqrt{-x^{2}+7 x-6}+x=4$.
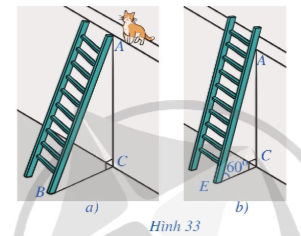
Bài tập 3. Để leo lên một bức tường, bác Nam dùng một chiếc thang có chiều dài cao hơn bức tường đó $1$m. Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên bức tường (Hình 33a). Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm $0,5$m thì bác Nam nhận thấy thang tạo với mặt đất một góc $60^{\circ}$ (Hình 33b). Hỏi bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
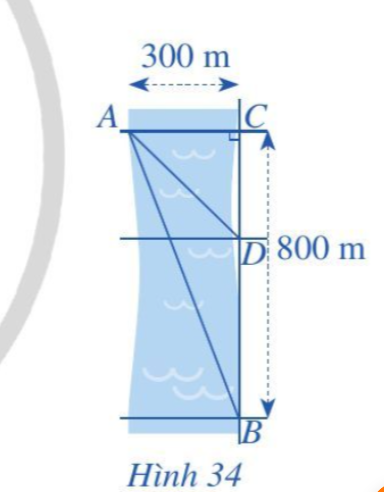
Bài tập 4. Một người đứng ở điểm $A$ trên một bờ sông rộng $300 \mathrm{~m}$, chèo thuyền đến vị trí $D$, sau đó chạy bộ đến vị trí $B$ cách $C$ một khoảng $800 \mathrm{~m}$ (Hình 34). Vận tốc chèo thuyền là $6 \mathrm{~km} / \mathrm{h}$, vận tốc chạy bộ là $10 \mathrm{~km} / \mathrm{h}$ và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí $C$ đến $D$, biết tổng thời gian người đó chèo thuyền và chạy bộ từ $A$ đến $B$ (qua $D$ ) là 7,2 phút.
Bài tập 5. Một ngọn hải đăng đặt tại vị trí $A$ cách bờ biển một khoảng cách $A B=4 \mathrm{~km}$. Trên bờ biển có một cái kho ở vị trí $C$ cách $B$ một khoảng là $7 \mathrm{~km}$. Người canh hải đăng có thể chèo thuyền từ $A$ đến vị trí $M$ trên bờ biển vối vận tốc $3 \mathrm{~km} / \mathrm{h}$ rồi đi bộ đến $C$ với vận tốc $5 \mathrm{~km} / \mathrm{h}$ (Hình 35 ). Tính khoảng cách từ vị trí $B$ đến $M$, biết thời gian người đó đi từ $A$ đến $C$ (qua $M$ ) là 148 phút.






