Giải bài tập 6 Tích vô hướng của hai vectơ
Giải bài tập 6 sách Giải bài tập 6 Tích vô hướng của hai vectơ
Sách "Giải bài tập 6 Tích vô hướng của hai vectơ" là một tài liệu hữu ích dành cho học sinh lớp 10, giúp họ hiểu rõ về cách tính tích vô hướng của hai vectơ và áp dụng vào các bài tập cụ thể.
Chương trình giáo khoa đưa ra các bài tập và sách này cung cấp phần đáp án chi tiết và hướng dẫn giải để học sinh có thể tự rèn luyện kỹ năng giải bài tập.
Với ví dụ đầu tiên, học sinh được yêu cầu tính tích vô hướng của hai vectơ trong tam giác vuông. Qua phần hướng dẫn giải, họ sẽ biết cách tính toán và áp dụng các kiến thức đã học để đạt được kết quả chính xác.
Đến ví dụ thứ hai, đây là bài tập về tam giác đều và đường cao. Hướng dẫn giải cung cấp cách tính tích vô hướng của hai vectơ trong trường hợp này và giúp học sinh hiểu rõ hơn về phương pháp giải bài tập khó hơn.
Bên cạnh đó, sách còn cung cấp những bài tập liên quan đến định lí Pythagore và cách chứng minh thông qua tích vô hướng của hai vectơ. Điều này giúp học sinh hình thành cách suy luận logic và tư duy toán học.
Với nội dung dễ hiểu, chi tiết và phong phú, sách Giải bài tập 6 Tích vô hướng của hai vectơ không chỉ giúp học sinh nắm vững kiến thức mà còn khơi gợi sự tò mò và đam mê với môn toán của họ.
Bài tập và hướng dẫn giải
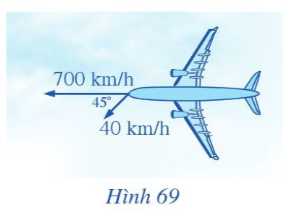
Bài tập 7. Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ $700 \mathrm{~km} / \mathrm{h}$ thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ $40 \mathrm{~km} / \mathrm{h}$ (Hình 69). Máy bay bị thay đổi vận tốc sau khi gặp gió thổi. Tìm tốc độ mới của máy bay theo đơn vị km/h (làm tròn kết quả đến hàng phần trăm).
Bài tập 8. Cho tam giác $A B C$ có $A B=2, A C=3, \widehat{B A C}=60^{\circ}$. Gọi $M$ là trung điểm của đoạn thẳng $B C$. Điểm $D$ thoả mãn $\overrightarrow{A D}=\frac{7}{12} \overrightarrow{A C}$.
a. Tính $\overrightarrow{A B} \cdot \overrightarrow{A C}$.
b. Biểu diễn $\overrightarrow{A M}, \overrightarrow{B D}$ theo $\overrightarrow{A B}, \overrightarrow{A C}$.
c. Chứng minh $A M \perp B D$.




