Giải bài tập 4 Bất phương trình bậc hai một ẩn
Giải bài tập 4 Bất phương trình bậc hai một ẩn
Trên đây là một số ví dụ và hướng dẫn giải bài tập về bất phương trình bậc hai một ẩn từ sách "Cánh diều toán lớp 10 tập 1".
Để bắt đầu, chúng ta làm quen với các bài tập cơ bản như $x^2-2x+2 > 0$ và $-x^2+5x-3 \leq 0$. Dùng các phương pháp giải tích hợp trong sách, ta có thể tìm ra tập nghiệm đúng cho từng bài tập.
Tiếp theo, chúng ta thực hành giải các bất phương trình bậc hai như $3x^2-2x+4 \leq 0$ và $-x^2+6x-9 \geq 0$. Qua các ví dụ này, chúng ta có thể hiểu cách giải bài toán và xác định tập nghiệm chính xác.
Ngoài ra, chúng ta cũng học cách sử dụng đồ thị để giải các bài toán như $x^2+2x+2>0$ và $-3x^2+2x-1>0$. Việc hình dung và phân tích đồ thị sẽ giúp chúng ta dễ dàng tìm tập nghiệm đúng cho bất phương trình đó.
Cuối cùng, chúng ta áp dụng kiến thức vào bài toán thực tế như tổng chi phí sản xuất sản phẩm và lãi nhuận. Bằng cách lập phương trình và tìm nghiệm, chúng ta có thể xác định số sản phẩm cần sản xuất để đảm bảo có lãi.
Hy vọng qua việc giải các bài tập này, các em học sinh sẽ nắm vững kiến thức và kỹ năng giải bài toán bất phương trình bậc hai một ẩn hiệu quả.
Bài tập và hướng dẫn giải
Bài tập 1. Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc hai một ẩn? Vì sao?
a. $-2 x+2<0$;
b. $\frac{1}{2} y^{2}-\sqrt{2}(y+1) \leq 0$;
c. $y^{2}+x^{2}-2 x \geq 0$.
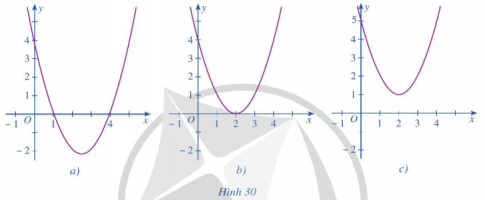
Bài tập 2. Dựa vào đồ thị hàm số bậc hai $y=f(x)$ trong mỗi Hình $30 a, 30 b$, 30c, hãy viết tập nghiệm của mỗi bất phương trình sau: $f(x)>0 ; f(x)<0 ; f(x) \geq 0 ; f(x) \leq 0$.
Bài tập 3. Giải các bất phương trình bậc hai sau:
a. $2 x^{2}-5 x+3>0$;
b. $-x^{2}-2 x+8 \leq 0$;
c. $4 x^{2}-12 x+9<0$;
d. $-3 x^{2}+7 x-4 \geq 0$.
Bài tập 4. Tìm $m$ để phương trình $2 x^{2}+(m+1) x+m-8=0$ có nghiệm.
Bài tập 5. Xét hệ tọa độ $Oth$ trên mặt phẳng, trong đó trục $Ot$ biểu thị thời gian $t$ (tính bằng giây) và trục $O h$ biểu thị độ cao $h$ (tính bằng mét). Một quả bóng được đá lên từ điểm $A(0 ; 0,2)$ và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8,5 m sau 1 giây và đạt độ cao 6 m sau 2 giây.
a. Hãy tìm hàm số bậc hai biểu thị quỹ đạo chuyển động của quả bóng.
b. Trong khoảng thời gian nào thì quả bóng vẫn chưa chạm đất?
Bài tập 6. Công ty An Bình thông báo giá tiền cho chuyến đi tham quan của một nhóm khách du lịch như sau:
10 khách đầu tiên có giá là 800000 đồng/người. Nếu có nhiều hơn 10 người đăng kí thì cứ có thêm 1 người, giá vé sẽ giảm 10000 đồng/người cho toàn bộ hành khách.
a. Gọi $x$ là số lượng khách từ người thứ 11 trở lên của nhóm. Biểu thị doanh thu theo $x$.
b. Số người của nhóm khách du lịch nhiều nhất là bao nhiêu thì công ty không bị lỗ? Biết rằng chi phí thực sự cho chuyến đi là 700000 đồng/người.