Giải bài tập sách bài tập (SBT) tin học lớp 10 kết nối tri thức bài 5: Dữ liệu logic
Giải bài tập sách bài tập (SBT) tin học lớp 10 kết nối tri thức - Bài 5: Dữ liệu logic
Trong phần này, chúng ta sẽ cùng nhau giải bài tập 5 về dữ liệu logic từ sách bài tập (SBT) tin học lớp 10 kết nối tri thức. Chúng ta sẽ có cơ hội tìm hiểu và hiểu rõ hơn về các khái niệm cơ bản của logic và cách áp dụng chúng vào việc giải các bài toán.
Chúng ta sẽ cung cấp đầy đủ đáp án chuẩn và hướng dẫn giải chi tiết từng bài tập. Hy vọng rằng thông qua việc thực hành, các em học sinh sẽ hiểu rõ hơn và nắm vững kiến thức bài học. Hãy cùng nhau đồng hành và khám phá thế giới logic thông qua bài tập này!
Bài tập và hướng dẫn giải
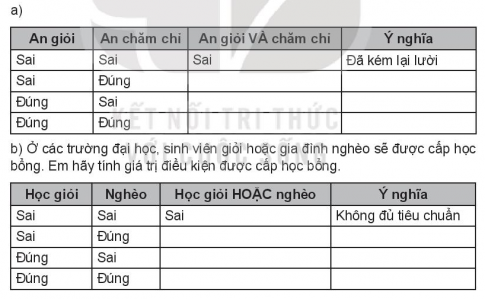
5.1. Em hãy điền vào ô trống trong bảng sau theo mẫu:
5.2. Trong thực tế, có nhiều đối tượng có hai trạng thái đối lập đều có thể quy về đại lượng logic như giới tính (nam hay nữ), tình trạng hôn nhân (độc thân hay đang kết hôn),...
Em hãy tìm thêm 3 ví dụ khác.
5.3. Một số hình vẽ trên mặt phẳng có thể biểu diễn qua các biểu thức logic có yếu tố tọa độ. Ví dụ Hình 5.1a được biểu diễn bởi biểu thức (x ≥ 0) AND (y ≥ 0) AND (x + y ≤ 1).
Em hãy viết biểu thức logic tương ứng với các Hình 5.1b, Hình 5.1c, Hình 5.1d.
5.4. Cho biểu thức lôgic (NOT x) AND (NOT y) như bảng sau. Em hãy cho biết kết quả nào sai?
| x | y | (NOT x) AND (NOT y) |
A | 0 | 0 | 1 |
B | 0 | 1 | 0 |
C | 1 | 0 | 1 |
D | 1 | 1 | 0 |
5.5. Em hãy tính giá trị của biểu thức lôgic (NOT x) OR (NOT y) với tất cả các bộ giá trị của x và y.
5.6. (*) Đố vui (Bài toán đoán màu mũ).
Chuyện rằng có 10 nhà thông thái (rất giỏi về suy luận lôgic) bị bọn cướp biển bắt được và giam trên đảo hoang. Chúng bịt mắt họ lại và đội lên đầu họ một chiếc mũ (đỏ hoặc xanh), sau đó bỏ băng bịt mắt. Mỗi người sẽ nhìn thấy và biết màu mũ của tất cả những người khác nhưng không biết màu mũ của mình.
Bọn cướp ra luật chơi, chúng sẽ hỏi từng người người xem họ đội mũ màu gì. Với điều kiện họ không được trao đổi với nhau, không được đoán mò, nếu chỉ một người đoán đúng, có cơ sở thì chúng sẽ tha tất, ngược lại sẽ tử hình toàn bộ.
Chúng hỏi nhà thông thái thứ nhất, ông nhìn tất cả những người còn lại và bảo không biết, không đủ cơ sở để biết màu mũ của mình. Chúng lại hỏi thông thái thứ hai, anh ta cũng trả lời không đủ cơ sở để biết màu mũ của mình.
Lần lượt cả 9 nhà thông thái đều trả lời rằng không đủ cơ sở để biết màu mũ của mình.
Đến nhà thông thái thứ mười, ông nói ngay màu mũ của mình và giải thích cách suy luận. Bọn cướp khâm phục và thả tất cả các nhà thông thái.
Em có biết, nhà thông thái thứ 10 đã suy luận thế nào không?





