Đề học sinh giỏi lớp 9 môn Toán năm 2022 2023 trường THCS Lý Nhật Quang Nghệ An (vòng 2)
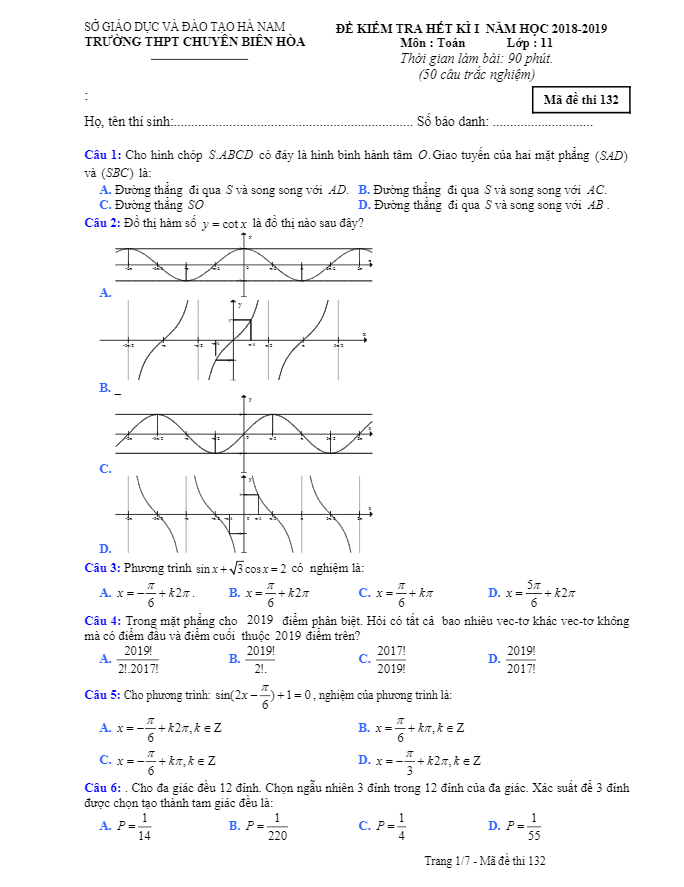
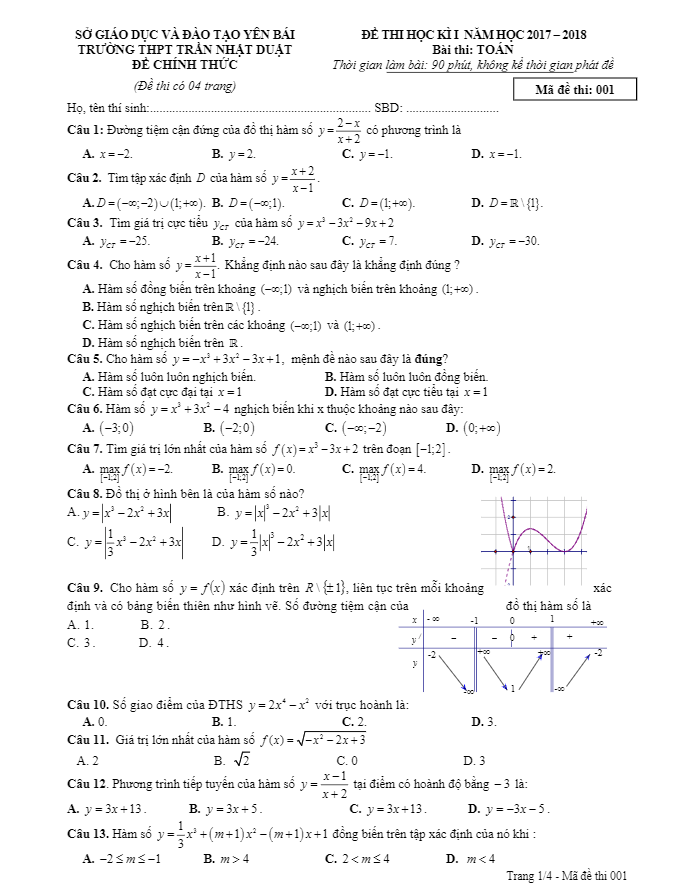
Nội dung Đề học sinh giỏi lớp 9 môn Toán năm 2022 2023 trường THCS Lý Nhật Quang Nghệ An (vòng 2) Bản PDF
Đề thi học sinh giỏi Toán lớp 9 trường THCS Lý Nhật Quang Nghệ An (vòng 2) năm 2022 - 2023
Xin chào quý thầy cô và các em học sinh lớp 9! Hôm nay, Sytu xin giới thiệu đến bạn đề thi chọn học sinh dự thi học sinh giỏi cấp tỉnh môn Toán lớp 9 năm học 2022-2023 tại trường THCS Lý Nhật Quang, huyện Đô Lương, tỉnh Nghệ An (vòng 2) với những câu hỏi thú vị và hấp dẫn sau:
1. Cho số nguyên tố P = abc với a, b, c là ba chữ số. Chứng minh rằng phương trình ax2 + bx + c = 0 không có nghiệm hữu tỷ.
2. Có tổng cộng 48 quả cân có khối lượng từ 1g đến 48g. Hãy phân chia tất cả các quả cân đó thành ba nhóm sao cho tổng khối lượng của từng nhóm bằng nhau.
3. Ban Giám hiệu trường THCS Lý Nhật Quang dự định mời 100 đại biểu đến dự sự kiện. Mỗi người trong số đó quen biết ít nhất 50 người khác. Chứng minh rằng Ban Giám Hiệu có thể xếp 4 người vào một bàn tròn sao cho mỗi người ngồi giữa hai người quen của mình.
Đây sẽ là một cơ hội tuyệt vời để các em thể hiện tài năng và kiến thức Toán của mình. Chúc các em học tập tốt và thành công trong kỳ thi sắp tới! Xin cám ơn!
Sách liên quan
Bạn có thể thích
Em rất biết ơn và trân trọng công sức mà thầy cô đã bỏ ra để biên soạn tài liệu này. Đây thực sự là một cơ hội tuyệt vời để phát triển bản thân và khẳng định tài năng của mình.
Tôi tin chắc rằng việc ôn tập thông qua những đề học sinh giỏi sẽ giúp các em nâng cao kỹ năng giải toán và chuẩn bị tốt nhất cho kỳ thi sắp tới.
Đọc đề nghĩa là phải suy nghĩ, phải tư duy và phải giải quyết vấn đề. Đây chính là lý do mà em cảm thấy háo hức khi được làm quen với những câu hỏi trong tài liệu này.
Tài liệu này thật sự là một cú hích lớn cho việc rèn luyện khả năng giải quyết vấn đề toán của em. Không chỉ giúp em nâng cao kiến thức mà còn rèn luyện tư duy logic và sự tự tin.
Em cảm thấy rất phấn khích khi được tiếp cận với đề học sinh giỏi này. Cảm ơn thầy cô đã tổ chức và chuẩn bị cho chúng em một cơ hội thực sự đáng quý!