Đề thi chọn học sinh giỏi lớp 10 môn Toán năm 2021 2022 sở GD ĐT Hà Nam
Nội dung Đề thi chọn học sinh giỏi lớp 10 môn Toán năm 2021 2022 sở GD ĐT Hà Nam Bản PDF
-
Nội dung bài viết
Đề thi chọn học sinh giỏi lớp 10 môn Toán năm 2021 2022 sở GD ĐT Hà Nam
Đề thi chọn học sinh giỏi môn Toán lớp 10 năm học 2021 – 2022 sở Giáo dục và Đào tạo tỉnh Hà Nam bao gồm 1 trang với 5 bài toán dạng tự luận, và thời gian làm bài là 180 phút.
Trích đề thi chọn học sinh giỏi Toán lớp 10 năm 2021 – 2022 sở GD&ĐT Hà Nam:
- Cho parabol \(y = x^2 + mx + m^2\) và đường thẳng \(2yx - my + m = 0\) (với m là tham số). Biết đường thẳng đó cắt parabol tại hai điểm phân biệt A và B. Tìm điều kiện của m để AB = 26.
- Cho phương trình \(2x^2 - bx + c = 0\) với b, c là số thực. Biết phương trình có hai nghiệm dương \(x_1, x_2\) thỏa mãn \(x_1 + x_2 = 4\).
- a) Chứng minh: \(b^2 - 4c > 0\)
- b) Tìm giá trị lớn nhất của biểu thức \(P = \frac{b^3}{6c} + \frac{b}{3} + 1\).
- Cho tam giác ABC nội tiếp đường tròn O bán kính R và có trọng tâm là G. Các đường thẳng AG, BG, CG theo thứ tự cắt đường tròn O tại điểm thứ hai là M, N, P. Biết \(\sin(A) + \sin(B) + \sin(C) = \frac{R}{2}\).
X
Sách liên quan
Bạn có thể thích
5 phút kiếm tiền mỗi ngày cùng SYTU
1.48143 sec| 2227.656 kb
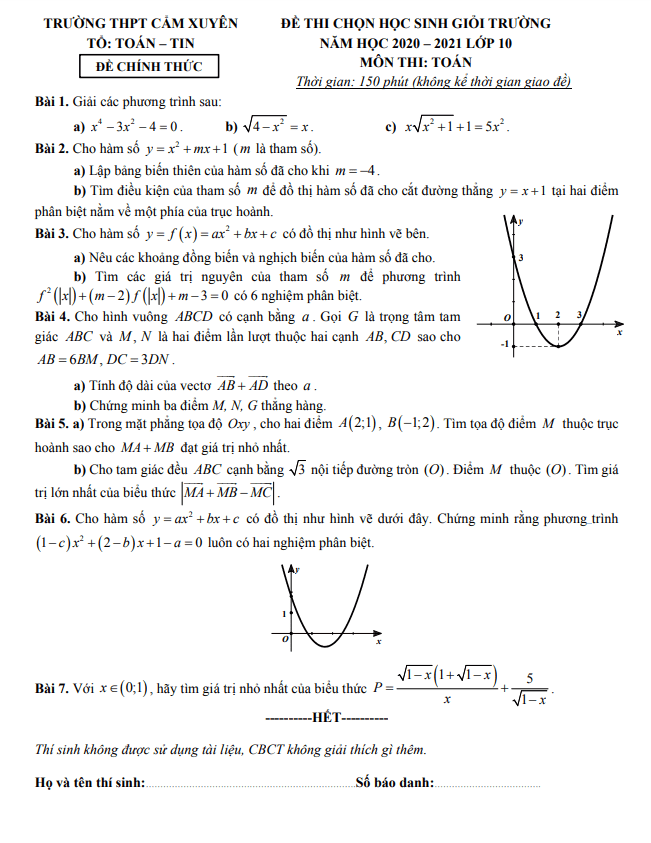
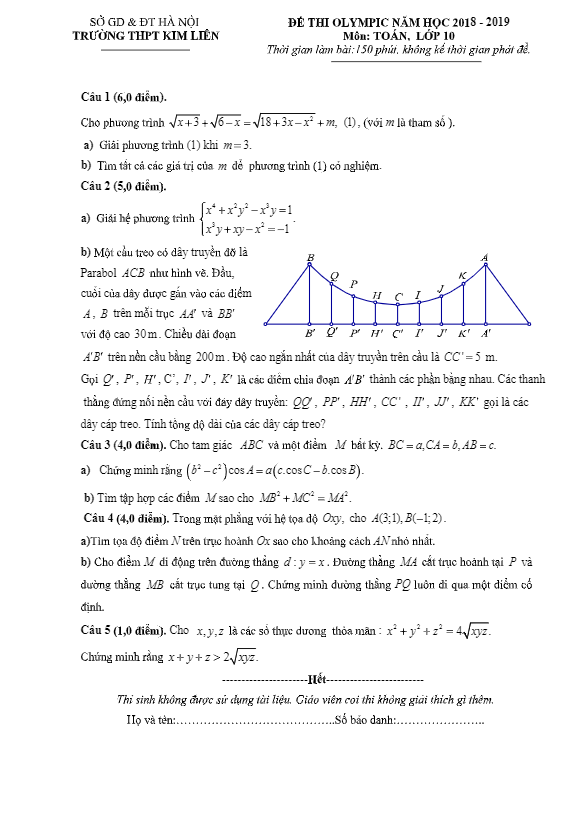
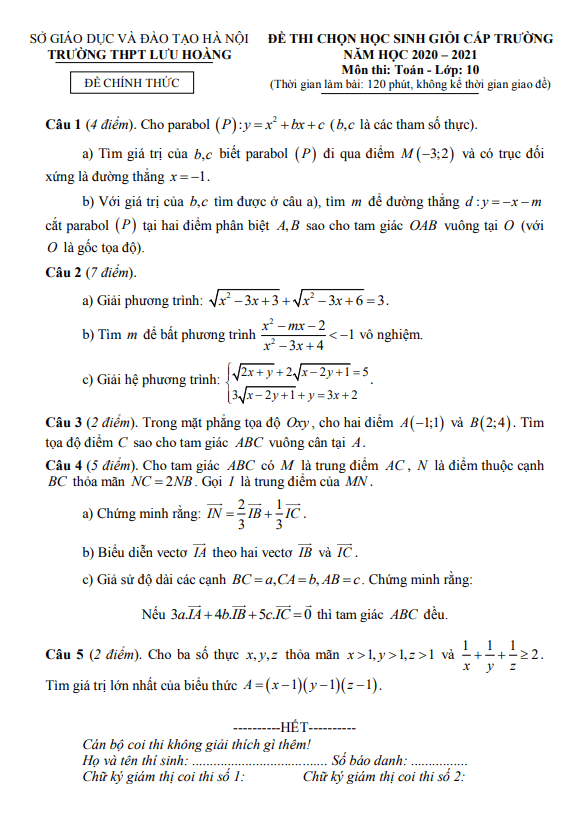
Tôi hy vọng rằng tài liệu này sẽ giúp học sinh lớp 10 ở Hà Nam phát triển tốt hơn trong môn Toán và có kết quả tốt ở các kì thi sắp tới.
Em không thể không đánh giá cao sự nỗ lực của những người đã làm ra tài liệu này, họ thật sự xứng đáng với sự đánh giá cao.
Tôi tin rằng nhờ tài liệu này, học sinh lớp 10 sẽ có cơ hội rèn luyện kỹ năng và kiến thức của mình.
Em rất biết ơn sở GD ĐT Hà Nam đã tổ chức và công bố tài liệu này để giúp các em ôn tập hiệu quả.
Tôi cảm động với sự chuẩn bị kỹ lưỡng và công phu trong việc biên soạn đề thi này.