Đề tuyển sinh chuyên môn Toán năm 2021 2022 sở GD ĐT Hải Phòng

Nội dung Đề tuyển sinh chuyên môn Toán năm 2021 2022 sở GD ĐT Hải Phòng Bản PDF
Nội dung bài viết
Đề tuyển sinh chuyên môn Toán năm 2021-2022 sở GD&ĐT Hải Phòng
Sytu xin gửi đến quý thầy, cô giáo và các em học sinh đề tuyển sinh lớp 10 chuyên môn Toán năm 2021-2022 sở GD&ĐT Hải Phòng. Đề thi bao gồm đáp án, lời giải chi tiết và hướng dẫn chấm điểm từ bảng chính thức do sở Giáo dục và Đào tạo thành phố Hải Phòng công bố.
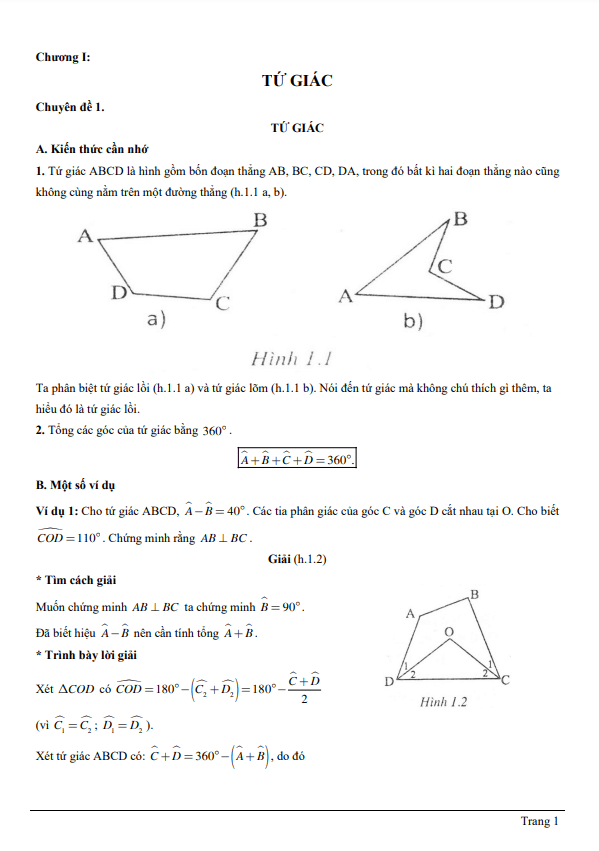
Trích dẫn đề tuyển sinh lớp 10 chuyên môn Toán năm 2021-2022 sở GD&ĐT Hải Phòng:
-
Cho hai phương trình (ẩn x; tham số a b). Tìm tất cả các cặp số thực (a;b) để mỗi phương trình trên đều có hai nghiệm phân biệt thỏa mãn 21x + 0 = x, trong đó 0 không phải là nghiệm của mỗi phương trình, và 1, 2 là hai nghiệm của từng phương trình.
-
Cho tam giác nhọn ABC (AB > AC) nội tiếp đường tròn (O). Gọi I là tâm đường tròn ngoại tiếp trong góc BAC của tam giác ABC. Đường thẳng AI cắt BC tại D, cắt đường tròn (O) tại E (E không phải là A). Chứng minh các điều kiện của tam giác ABC.
-
Cho tập hợp X = {1, 2, 3, ..., 101}. Tìm số tự nhiên n (n ≥ 3) nhỏ nhất sao cho với mọi tập con A tùy ý gồm n phần tử của X sẽ tồn tại 3 phần tử đôi một phân biệt abc thỏa mãn abc.
Đề tuyển sinh này sẽ giúp các em học sinh ôn tập và củng cố kiến thức Toán một cách hiệu quả, chuẩn bị tốt nhất cho kỳ thi sắp tới. Mong rằng đề thi sẽ mang lại những thử thách thú vị và khám phá cho các em.

























Tôi cảm thấy rất tự hào vì sở GD ĐT Hải Phòng đã chia sẻ tài liệu đề tuyển sinh Toán. Điều này giúp học sinh có thêm nguồn lực để học tập và nâng cao kiến thức của mình.
Em rất hào hứng khi được tiếp cận với tài liệu đề tuyển sinh Toán của sở GD ĐT Hải Phòng. Đây chắc chắn sẽ là bước ngoặt quan trọng trong việc chuẩn bị cho kỳ thi.
Tôi tin chắc rằng tài liệu này sẽ giúp học sinh tự tin hơn trong kỳ thi tuyển sinh sắp tới. Đây là cơ hội để họ thể hiện kiến thức và kỹ năng mình đã học.
Em thấy rất cảm động khi thấy có nguồn tài liệu chuyên môn như vậy. Đây sẽ là cơ hội tốt để học sinh rèn luyện và phát triển khả năng Toán của mình.
Tôi muốn bày tỏ lòng biết ơn đến sở GD ĐT Hải Phòng vì đã chuẩn bị tài liệu chất lượng như vậy cho học sinh. Điều này thật sự tạo điều kiện thuận lợi cho việc ôn tập và nâng cao kiến thức.