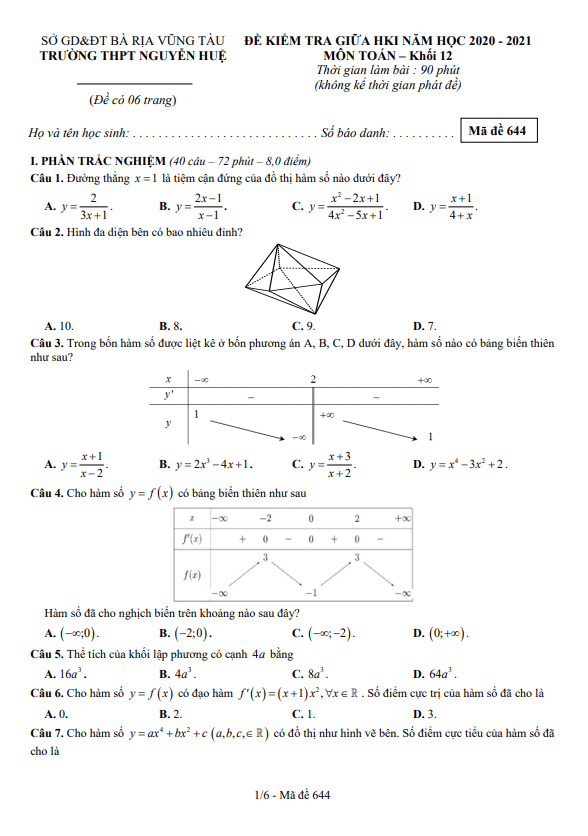
Đề chọn đội tuyển thi HSG Quốc gia môn Toán năm 2020 2021 sở GD ĐT Kiên Giang

Nội dung Đề chọn đội tuyển thi HSG Quốc gia môn Toán năm 2020 2021 sở GD ĐT Kiên Giang Bản PDF

Đề chọn đội tuyển thi HSG Quốc gia môn Toán năm 2020-2021

Ngày 29 tháng 09 năm 2020, sở Giáo dục và Đào tạo tỉnh Kiên Giang đã tổ chức kỳ thi chọn đội tuyển dự thi học sinh giỏi môn Toán cấp Quốc gia cho năm học 2020-2021. Đề chọn đội tuyển thi HSG Quốc gia môn Toán năm 2020-2021 của sở GD&ĐT Kiên Giang bao gồm 01 trang với 04 bài toán tự luận. Thời gian làm bài thi là 180 phút (không tính thời gian phát đề).

Trích dẫn từ đề chọn đội tuyển thi HSG Quốc gia môn Toán năm 2020-2021 sở GD&ĐT Kiên Giang:

Bài 1: Cho đường tròn (C1) và điểm B thuộc (C1). Điểm A khác B sao cho đường thẳng AB là tiếp tuyến của (C1). Điểm C không thuộc (C1) sao cho đoạn thẳng AC cắt (C1) tại hai điểm phân biệt. Gọi (C2) là đường tròn tiếp xúc với AC tại C và tiếp xúc với (C1) tại D (điểm B và D nằm ở hai phía khác so với bờ AC). Gọi I là tâm đường tròn ngoại tiếp tam giác BCD và delta là tiếp tuyến chung của (C1), (C2) tại D. a) Chứng minh rằng điểm I cách đều hai đường thẳng AB và delta. b) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác BCD nằm trên đường tròn ngoại tiếp tam giác ABC.

Bài 2: Trên tập hợp các số nguyên không âm, xét phương trình: x^2 + 2.3^y = x(2^(y + 1) - 1) a) Tìm tất cả các cặp số nguyên không âm (x;y) thỏa mãn phương trình trên với y ≤ 5. b) Chứng minh rằng không tồn tại cặp số nguyên không âm (x;y) với y ≥ 6 thỏa mãn phương trình.

Bài 3: Tìm tất cả các hàm số liên tục f: R → R sao cho: 8f(4x) - 10f(2x) + 3f(x) = 30x với mọi x thuộc R.