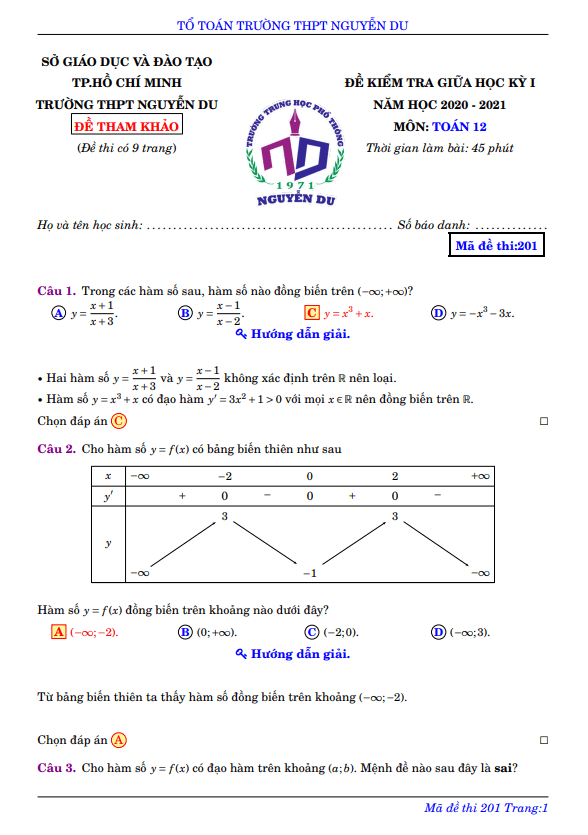
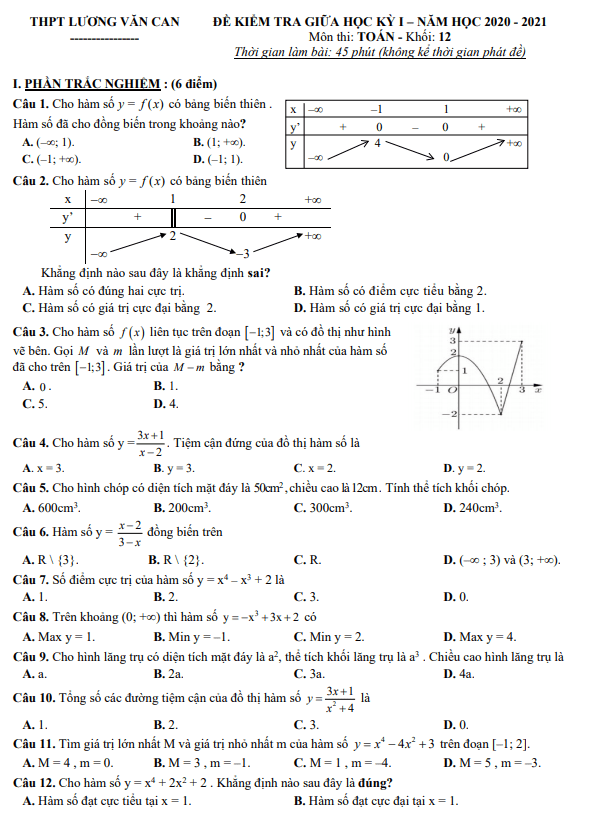
Đề thi tham khảo giữa HKI lớp 12 môn Toán năm 2020 2021 trường THPT Nguyễn Du TP HCM

Nội dung Đề thi tham khảo giữa HKI lớp 12 môn Toán năm 2020 2021 trường THPT Nguyễn Du TP HCM Bản PDF

Đề thi tham khảo giữa HKI lớp 12 môn Toán năm 2020-2021 trường THPT Nguyễn Du TP HCM

Để giúp các em học sinh lớp 12 chuẩn bị cho kỳ thi khảo sát chất lượng giữa học kỳ 1 môn Toán sắp tới, Sytu xin giới thiệu đến các em đề thi tham khảo giữa HKI Toán lớp 12 năm học 2020-2021 của trường THPT Nguyễn Du, thành phố Hồ Chí Minh.

Đề thi bao gồm 25 câu trắc nghiệm, thời gian làm bài 45 phút. Đề thi có đáp án và lời giải chi tiết để các em tham khảo sau khi làm bài.

Dưới đây là một số câu hỏi mẫu trong đề thi:

Câu 1: Cho hàm số y = f(x) có đạo hàm trên khoảng (a, b). Mệnh đề nào sau đây là sai? A. Nếu f'(x) < 0 với mọi x thuộc (a, b) thì hàm số y = f(x) nghịch biến trên (a, b). B. Nếu f'(x) > 0 với mọi x thuộc (a, b) thì hàm số y = f(x) đồng biến trên (a, b). C. Nếu hàm số y = f(x) nghịch biến trên (a, b) thì f'(x) ≤ 0 với mọi x thuộc (a, b). D. Nếu hàm số y = f(x) đồng biến trên (a, b) thì f'(x) > 0 với mọi x thuộc (a, b).

Câu 2: Cho hàm số f(x) liên tục trên khoảng D ⊂ R và x0 thuộc D. Mệnh đề nào sau đây là đúng? A. x0 là điểm cực đại của hàm số f nếu f(x) > f(x0) với mọi x thuộc D. B. x0 là điểm cực đại của hàm số f nếu với mọi (a, b) ⊂ D chứa x0 ta đều có f(x) > f(x0) với mọi x thuộc (a, b)\{x0}. C. x0 là cực đại của hàm số f nếu tồn tại (a, b) ⊂ D chứa x0 sao cho f(x) < f(x0) với mọi x thuộc (a, b)\{x0}. D. x0 là điểm cực đại của hàm số f nếu f(x) < f(x0) với mọi x thuộc (a, b) ⊂ D.

Câu 3: Cho hàm số y = f(x) có bảng biến thiên như sau. Xét các mệnh đề sau: (I). Hàm số f(x) đồng biến trên khoảng (-∞, 2). (II). Hàm số y = f(x) đồng biến trên R. (III). Hàm số không có cực trị. Số các mệnh đề đúng là?

Các em hãy tự làm và kiểm tra đáp án trong đề thi để tự đánh giá và cải thiện kiến thức của mình trong môn Toán. Chúc các em thành công!