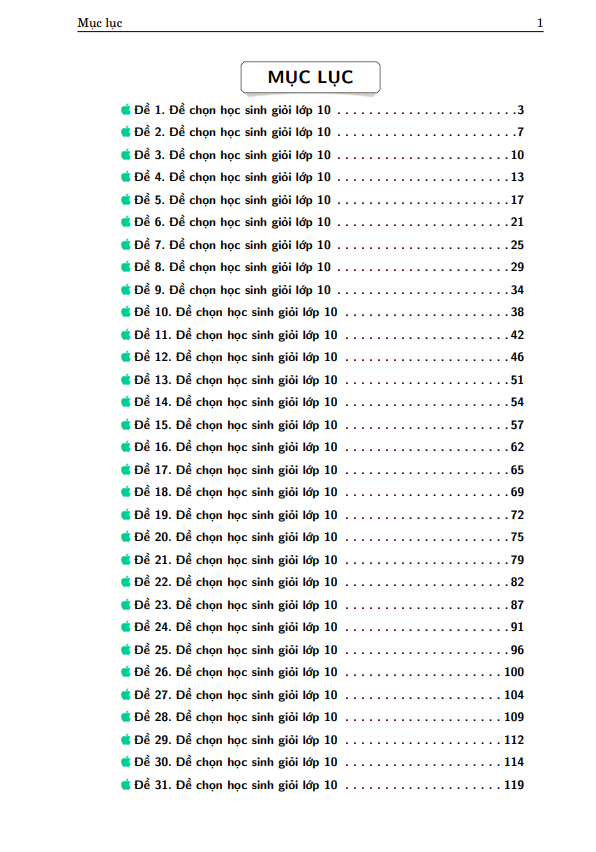
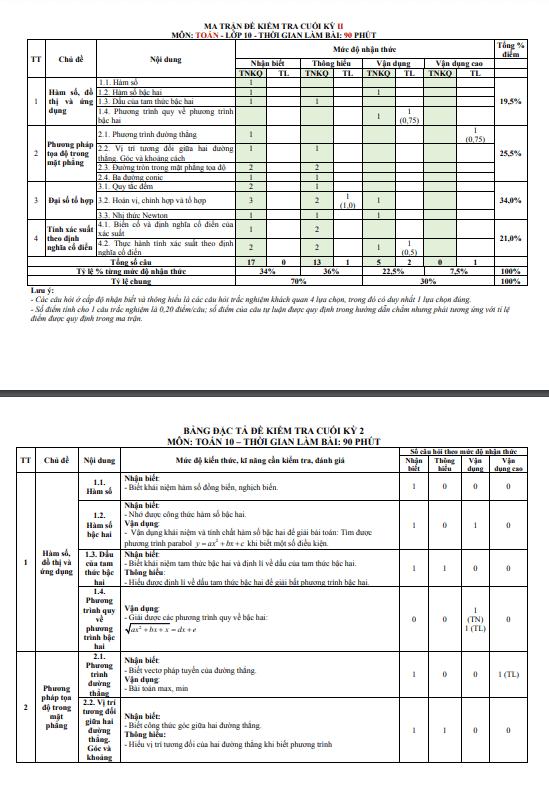
Đề thi chọn HSG cấp tỉnh lớp 12 môn Toán năm 2018 2019 sở GD và ĐT Bình Thuận (Vòng 2)

Nội dung Đề thi chọn HSG cấp tỉnh lớp 12 môn Toán năm 2018 2019 sở GD và ĐT Bình Thuận (Vòng 2) Bản PDF

Đề thi chọn HSG cấp tỉnh Toán lớp 12 năm 2018 – 2019 sở GD và ĐT Bình Thuận (Vòng 2)

Đề thi chọn HSG cấp tỉnh Toán lớp 12 năm 2018 – 2019 sở GD và ĐT Bình Thuận (Vòng 2) bao gồm 1 trang với 4 bài toán tự luận, thời gian làm bài 180 phút. Kỳ thi được diễn ra vào ngày 19 tháng 10 năm 2018 nhằm thành lập đội tuyển học sinh giỏi Toán lớp 12 dự thi Quốc gia. Đề thi này cung cấp lời giải chi tiết và thang chấm điểm.

Trích dẫn một bài toán trong đề thi: Cho tam giác ABC có AB < AC và nội tiếp đường tròn (O). Qua góc BAC, vẽ phân giác và ký hiệu giao điểm với (O) là D. Từ B, vẽ đường thẳng đi qua E đối xứng của B qua AD, cắt (O) tại F. Kế tiếp, vẽ BG cắt (O) tại H. Đường thẳng qua C song song với AH cắt FD tại I. Trên EO, vẽ đường tròn ngoại tiếp tam giác BCG, cắt EI tại K và L. Chứng minh đường trung trực của đoạn thẳng KL luôn đi qua một điểm cố định.

Bên cạnh đó, còn một bài toán khác: Cho 2018 tập hợp mỗi tập chứa 45 phần tử, mỗi cặp tập đều có một phần tử chung. Hãy chứng minh rằng tồn tại một phần tử thuộc vào tất cả 2018 tập hợp đã cho.