Lý thuyết và bài tập chuyên đề hàm số

Mời thí sinh CLICK vào liên kết hoặc ảnh bên dưới
Mở ứng dụng Shopee để tiếp tục làm bài thi
https://s.shopee.vn/AKN2JyAJAw
https://s.shopee.vn/AKN2JyAJAw
Sytu.vn và đội ngũ nhân viên xin chân thành cảm ơn!
X
1.62710 sec| 2404.797 kb














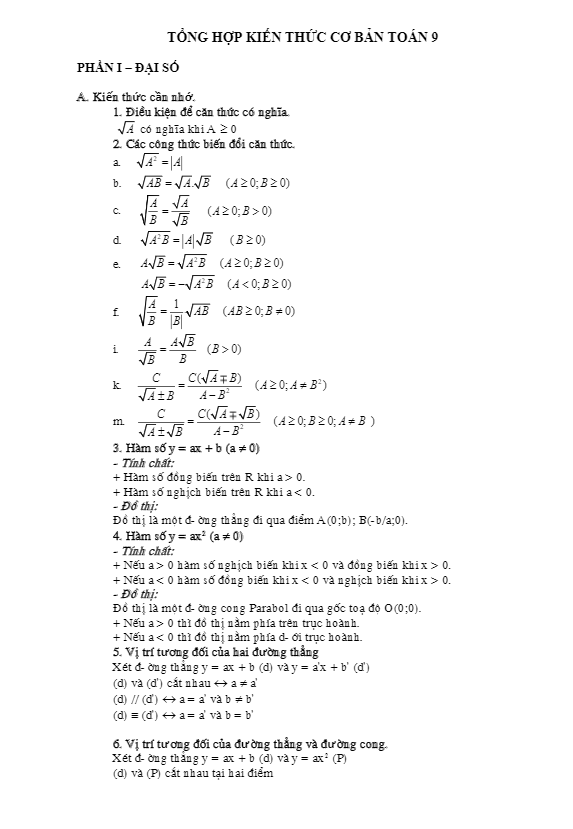






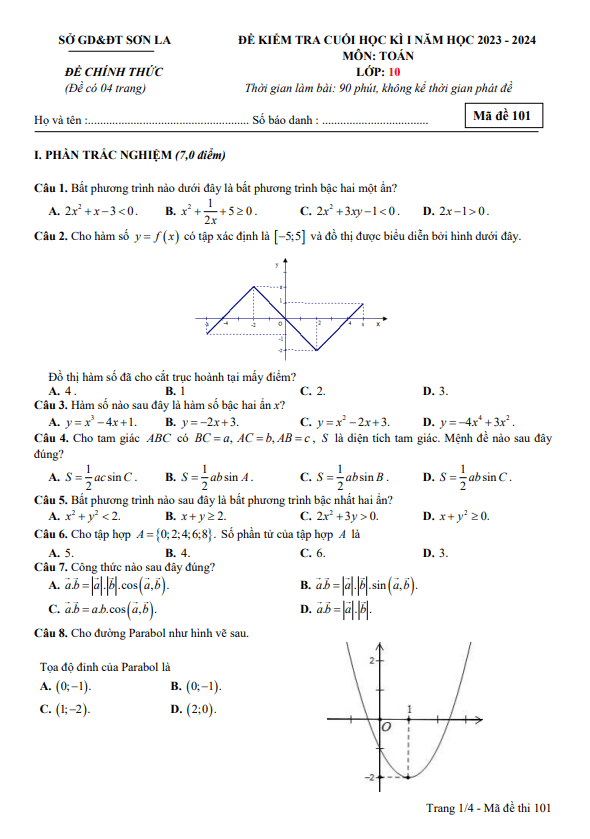

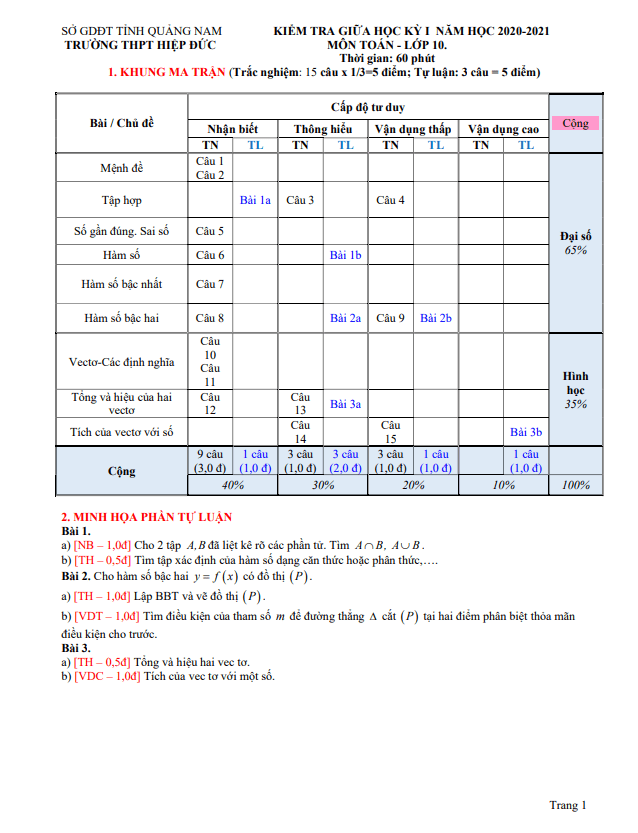

Em đọc qua tài liệu và thấy rằng nó thực sự hữu ích cho việc ôn tập và rèn luyện kỹ năng giải bài tập về hàm số. Cảm ơn tác giả rất nhiều!
Tôi đã download tài liệu này và không thể không chia sẻ với các bạn học cùng lớp. Chắc chắn họ cũng sẽ rất hứng thú với nó.
Nội dung của tài liệu rất dễ tiếp cận và hấp dẫn, giúp em thấy khái niệm về hàm số trở nên rõ ràng hơn bao giờ hết.
Mỗi bài tập trong tài liệu đều rất thú vị và mang lại nhiều kiến thức mới. Tôi sẽ dành thời gian học hỏi từ những bài tập này.
Tài liệu này thật sự là một nguồn thông tin quý giá đối với những ai đam mê toán học. Tôi thật sự rất biết ơn tác giả đã biên soạn nó.