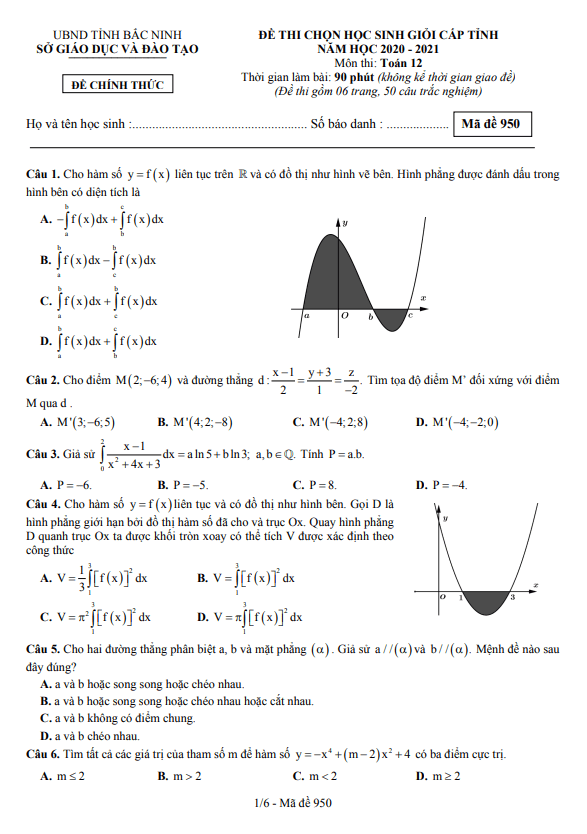
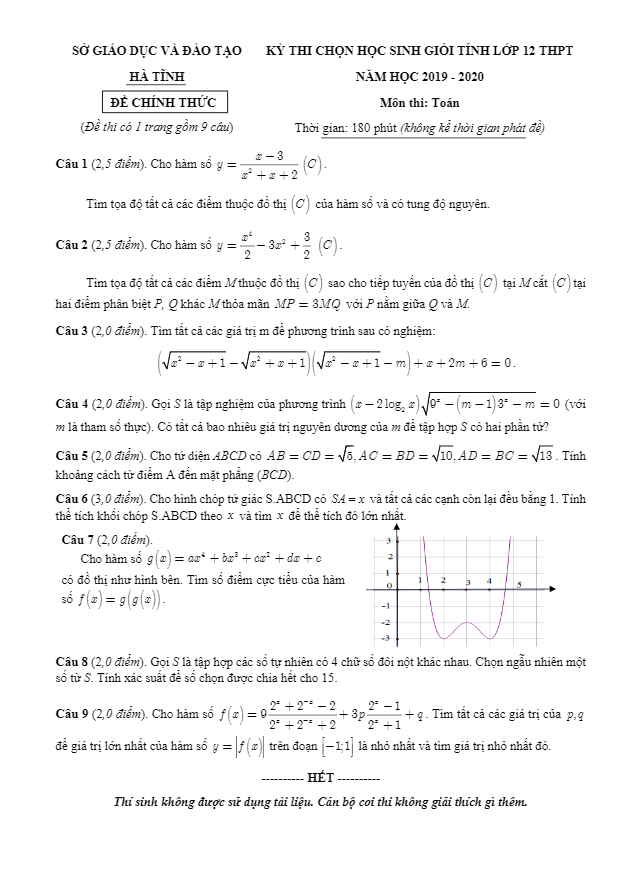
Đề học sinh giỏi lớp 12 môn Toán chuyên năm 2023 2024 sở GD ĐT Vĩnh Phúc

Nội dung Đề học sinh giỏi lớp 12 môn Toán chuyên năm 2023 2024 sở GD ĐT Vĩnh Phúc Bản PDF
Nội dung bài viết
Đề thi học sinh giỏi Toán lớp 12 chuyên năm 2023-2024 sở GD&ĐT Vĩnh Phúc
Xin chào quý thầy cô và các em học sinh lớp 12! Đây là đề thi chọn học sinh giỏi môn Toán lớp 12 THPT chuyên năm học 2023-2024 của sở Giáo dục và Đào tạo tỉnh Vĩnh Phúc.
1. Cho số nguyên dương n lớn hơn 1. Ký hiệu G(n) là ước nguyên tố lớn nhất của n. a) Chứng minh rằng nếu n + 1 là lũy thừa của 2 và n chia hết cho 11 thì G(n) > 11. b) Hai số nguyên tố phân biệt p, q được gọi là xa lạ nếu không tồn tại số nguyên dương n lớn hơn 1 sao cho hai tập hợp {p;q} và {G(n);G(n + 1)} trùng nhau. Chứng minh rằng nếu p < q là hai số nguyên tố lẻ sao cho ordp2 = ordq2 thì 2 và p là hai số xa lạ và có vô hạn cặp số nguyên tố (p;9) sao cho p < q và hai số p và q là xa lạ.
2. Cho tam giác ABC nhọn và cân tại đỉnh A. Gọi D và E lần lượt là trung điểm của CB và CA, M là trung điểm của DE. Đường tròn ngoại tiếp tam giác AEM cắt cạnh AB tại điểm N. Tiếp tuyến tại M và N của đường tròn ngoại tiếp tam giác AEM cắt nhau tại P. a) Đường thẳng AM cắt tiếp tuyến tại E của đường tròn ngoại tiếp tam giác AEM ở điểm Q. Chứng minh rằng P, D, Q thẳng hàng. b) Chứng minh rằng điểm P nằm trên đường thẳng BC.
3. Cho số nguyên dương n > 1, số nguyên dương k được gọi là n-good nếu với mọi cách tô màu mỗi số nguyên dương từ 1 đến k bởi một trong hai màu xanh hoặc đỏ, ta luôn chọn được n số cùng màu sao cho tổng của n số này cũng nằm trong tập hợp {1; 2; ...; k} và cùng màu với n số vừa chọn. a) Tìm số 2-good nhỏ nhất. b) Tìm số 2024-good nhỏ nhất.
Hãy cùng nhau giải các bài toán thú vị này để rèn luyện tư duy logic và kỹ năng giải quyết vấn đề trong môn Toán. Chúc các bạn thành công!