VI. Liên hệ giữa đường tròn và đường elipHoạt động 8.Cho elip (E) có phương trình chính tắc...
Câu hỏi:
VI. Liên hệ giữa đường tròn và đường elip
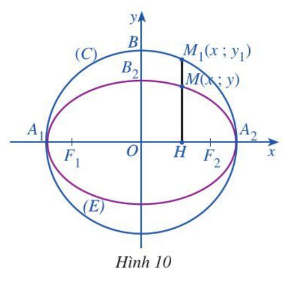
Hoạt động 8. Cho elip (E) có phương trình chính tắc là $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ (a > b > 0). Xét đường tròn (C) tâm O bán kính a có phương trình là $x^{2} + y^{2} = a^{2}$.
Xét điểm M(x; y) ∈ (E) và điểm M1(x; y1) ∈ (C) sao cho y và y1 luôn cùng dấu (khi M khác với hai đỉnh A1, A2 của (E)) (Hình 10).
a) Từ phương trình chính tắc của elip (E), hãy tính $y^{2}$ theo $x^{2}$.
Từ phương trình của đường tròn (C), hãy tính $y1^{2}$ theo $x^{2}$.
b) Tính tỉ số $\frac{HM}{HM1}=\frac{y}{y1}$ theo a và b.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Huy
Để giải câu hỏi trên, ta cần thực hiện các bước sau đây:
a) Để tính $y^2$ theo $x^2$ từ phương trình chính tắc của elip (E), ta có:
$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
$\Rightarrow \frac{y^2}{b^2} = 1 + \frac{x^2}{a^2} = \frac{a^2 - x^2}{a^2}$
$\Rightarrow y^2 = \frac{(a^2 - x^2)b^2}{a^2}$
Để tính $y_1^2$ theo $x^2$ từ phương trình đường tròn (C), ta có:
$x^2 + y_1^2 = a^2$
$\Rightarrow y_1^2 = a^2 - x^2$
b) Ta cần tính tỉ số $\frac{HM}{HM_1} = \frac{y}{y_1}$ theo $a$ và $b$. Từ phần a), ta đã có các kết quả sau:
$y^2 = \frac{(a^2 - x^2)b^2}{a^2}$ và $y_1^2 = a^2 - x^2$
Suy ra:
$\frac{y^2}{y_1^2} = \frac{\frac{(a^2 - x^2)b^2}{a^2}}{a^2 - x^2} = \frac{b^2}{a^2}$
$\Rightarrow \frac{y}{y_1} = \frac{b}{a}$
Vậy, tỉ số $\frac{HM}{HM_1} = \frac{y}{y_1} = \frac{b}{a}$.
Câu trả lời đầy đủ và chi tiết hơn là:
a) Tính được:
$y^2 = \frac{(a^2 - x^2)b^2}{a^2}$ và $y_1^2 = a^2 - x^2$
b) Tỉ số $\frac{HM}{HM_1} = \frac{y}{y_1} = \frac{b}{a}$
a) Để tính $y^2$ theo $x^2$ từ phương trình chính tắc của elip (E), ta có:
$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
$\Rightarrow \frac{y^2}{b^2} = 1 + \frac{x^2}{a^2} = \frac{a^2 - x^2}{a^2}$
$\Rightarrow y^2 = \frac{(a^2 - x^2)b^2}{a^2}$
Để tính $y_1^2$ theo $x^2$ từ phương trình đường tròn (C), ta có:
$x^2 + y_1^2 = a^2$
$\Rightarrow y_1^2 = a^2 - x^2$
b) Ta cần tính tỉ số $\frac{HM}{HM_1} = \frac{y}{y_1}$ theo $a$ và $b$. Từ phần a), ta đã có các kết quả sau:
$y^2 = \frac{(a^2 - x^2)b^2}{a^2}$ và $y_1^2 = a^2 - x^2$
Suy ra:
$\frac{y^2}{y_1^2} = \frac{\frac{(a^2 - x^2)b^2}{a^2}}{a^2 - x^2} = \frac{b^2}{a^2}$
$\Rightarrow \frac{y}{y_1} = \frac{b}{a}$
Vậy, tỉ số $\frac{HM}{HM_1} = \frac{y}{y_1} = \frac{b}{a}$.
Câu trả lời đầy đủ và chi tiết hơn là:
a) Tính được:
$y^2 = \frac{(a^2 - x^2)b^2}{a^2}$ và $y_1^2 = a^2 - x^2$
b) Tỉ số $\frac{HM}{HM_1} = \frac{y}{y_1} = \frac{b}{a}$
Câu hỏi liên quan:
- I. Tính đối xứng của ElipHoạt động 1.Trong mặt phẳng toạ độ Oxy, ta xét elip (E) có phương...
- Hoạt động 2.Trong mặt phẳng toạ độ Oxy, ta xét elip (E) có phương trình chính tắc là...
- II. Hình chữ nhật cơ sởHoạt động 3.a) Nêu nhận xét về vị trí bốn đỉnh của elip (E) với bốn...
- Luyện tập 1.Viết phương trình chính tắc của elip, biết A1(– 4; 0) và B2(0; 2) là hai đỉnh của...
- Hoạt động 4.Quan sát elip (E) có phương trinh chính tắc là...
- III. Tâm sai của ElipLuyện tập 2.Viết phương trình chính tắc của elip (E), biết tiêu cự bằng...
- IV. Bán kính qua tiêu của một điểm thuộc elipHoạt động 5.Giả sử đường elip (E) là tập hợp các...
- Hoạt động 6.Sử dụng đẳng thức c) ở trên và đẳng thức MF1+ MF2= 2a, chứng minh:a)...
- Luyện tập 3.Cho elip (E): $\frac{x^{2}}{9}+\frac{y^{2}}{4}=1$với tiêu điểm...
- Luyện tập 3.Cho elip (E): $\frac{x^{2}}{9}+\frac{y^{2}}{4}=1$với tiêu điểm...
- V. Đường chuẩn của ElipHoạt động 7.Cho elip (E) có phương trình chính tắc là...
- Luyện tập 4.Viết phương trình chính tắc của elip, biết tiêu điểm F2(5; 0) và đường chuẩn ứng...
- VII. Cách vẽ đường ElipHoạt động 9.Vẽ elip (E): $\frac{x^{2}}{25}+\frac{y^{2}}{9}=1$
- Bài tậpBài tập 1.Viết phương trình chính tắc của elip (E) trong mỗi trường hợp sau:a) Độ dài...
- Bài tập 2.Tìm tâm sai của elip (E) trong mỗi trường hợp sau:a) Độ dài bán trục lớn gấp hai...
- Bài tập 3.Trái Đất chuyển động quanh Mặt Trời theo một quỹ đạo là đường elip mà Mặt Trời là...
- Bài tập 4.Cho elip (E): $\frac{x^{2}}{25}+\frac{y^{2}}{9}=1$Tìm toạ độ điểm M...
- Bài tập 5.Hình 11 minh hoạ mặt cắt đứng của một căn phòng trong bảo tàng với mái vòm trần nhà...
Bình luận (0)





