Luyện tập 1 trang 32 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hình chóp S.ABCD có đáy...
Câu hỏi:
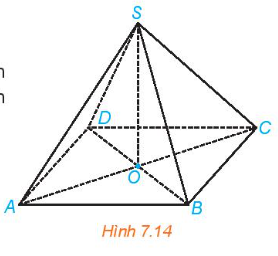
Luyện tập 1 trang 32 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, SA = SC và SB = SD (H.7.14). Chứng minh rằng $SO\perp (ABCD)$.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Giang
Để chứng minh rằng $SO \perp (ABCD)$, ta có thể giải bằng phương pháp sau:
Vì $ABCD$ là hình bình hành nên $OA=OC$ và $OB=OD$. Từ $SA = SC$ và $SB = SD$, ta có $\triangle SAB=\triangle SDC$Suy ra $\angle SBA = \angle SCD$. Tương tự, từ $SA = SC$ và $SB = SD$, ta có $\triangle SAC = \triangle SBD$ Suy ra $\angle SAC = \angle SBD$. Do đó, $\angle BSC = \angle SBD + \angle SCD = \angle SAC + \angle SBA = 180^\circ - \angle AOB$.
Mà $\angle BOC = 180^\circ$, nên $\angle BOS = \angle COS = \frac{\angle BOC}{2}$.
Từ đó suy ra $\angle BOS + \angle BSC = 90^\circ$, tức $SO \perp (ABCD)$.
Vậy, ta đã chứng minh được $SO$ vuông góc với $(ABCD)$.
Vì $ABCD$ là hình bình hành nên $OA=OC$ và $OB=OD$. Từ $SA = SC$ và $SB = SD$, ta có $\triangle SAB=\triangle SDC$Suy ra $\angle SBA = \angle SCD$. Tương tự, từ $SA = SC$ và $SB = SD$, ta có $\triangle SAC = \triangle SBD$ Suy ra $\angle SAC = \angle SBD$. Do đó, $\angle BSC = \angle SBD + \angle SCD = \angle SAC + \angle SBA = 180^\circ - \angle AOB$.
Mà $\angle BOC = 180^\circ$, nên $\angle BOS = \angle COS = \frac{\angle BOC}{2}$.
Từ đó suy ra $\angle BOS + \angle BSC = 90^\circ$, tức $SO \perp (ABCD)$.
Vậy, ta đã chứng minh được $SO$ vuông góc với $(ABCD)$.
Câu hỏi liên quan:
- 1. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNGHoạt động 1 trang 31 sách giáo khoa (SGK) toán lớp 11 tập 2...
- Hoạt động 2 trang 32 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Gấp tấm bìa cứng hình chữ...
- Vận dụng trang 33 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Khi làm cột treo quần áo, ta có...
- 2. TÍNH CHẤTHoạt động 3 trang 33 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho điểm O và...
- Hoạt động 4 trang 34 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho mặt phẳng (P) và điểm O....
- Luyện tập 2 trang 34 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho ba điểm phân biệt A, B,...
- 3. LIÊN HỆ GIỮA QUAN HỆ SONG SONG VÀ QUAN HỆ VUÔNG GÓC CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNGHoạt động 5...
- Hoạt động 6 trang 34 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hai đường thẳng phân...
- Hoạt động 7 trang 35 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hai mặt phẳng (P) và...
- Hoạt động 8 trang 35 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hai mặt phẳng phân biệt...
- Luyện tập 3 trang 35 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Một chiếc bàn có các chân...
- Hoạt động 9 trang 35 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho đường thẳng a song song...
- Hoạt động 10 trang 36 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho đường thẳng a và mặt...
- Luyện tập 4 trang 36 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hình chóp S.ABCD có đáy...
- BÀI TẬPBài tập 7.5 trang 36 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hình chóp S.ABC...
- Bài tập 7.6 trang 36 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hình chóp S.ABCD có đáy...
- Bài tập 7.7 trang 36 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hình chóp S.ABCD có đáy...
- Bài tập 7.8 trang 36 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Bạn Vinh thả quả dọi chìm...
- Bài tập 7.9 trang 36 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Một cột bóng rổ được dựng...
Bình luận (0)





