Câu 2: Cho hàm số y = x + 1 có đồ thị là (d) và hàm số y = -x + 3 có đồ thị là (d'). a/ Vẽ (d) và (d') trên cùng một mặt phẳng tọa độ. b/ Hai đường thẳng (d) và (d')  cắt nhau tại Cvà cắt trục Ox lần lượt tại A và B. Dựa vào đồ thị tìm tọa độ các điểm A, B, C. c/ Tính chu vi và diện tích của tam giác ABC   ( GIẢNG CHO MÌNH CÁCH LÀM TỪNG BƯỚC ĐƯỢC KHÔNG Ạ ) :((((
Chào các Bạn, mình đang gặp một chút vấn đề và thực sự cần sự trợ giúp của mọi người. Bạn nào biết cách giải quyết không, có thể chỉ giúp mình được không?

a: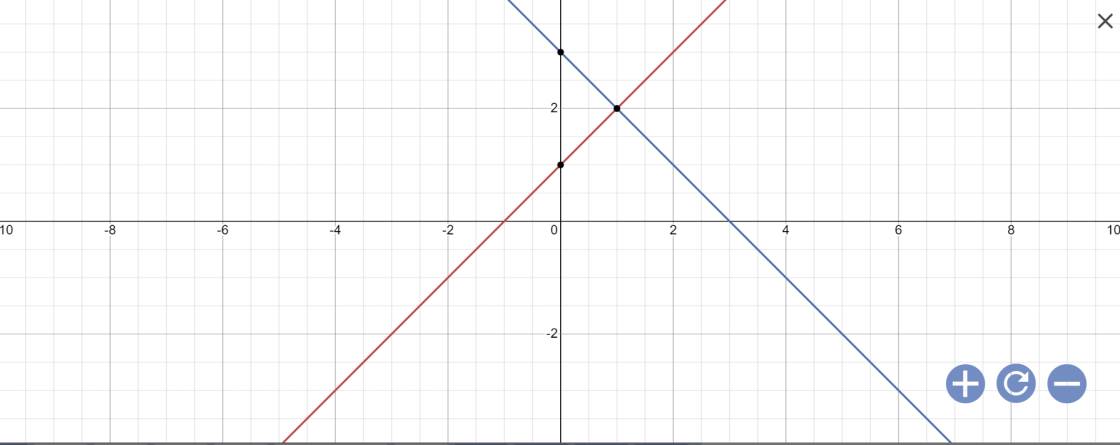

b: tọa độ C là:

\(\left\{{}\begin{matrix}x+1=-x+3\\y=x+1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x=2\\y=x+1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=1\\y=1+1=2\end{matrix}\right.\)

Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\x+1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)

Tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)

Vậy: A(-1;0); B(3;0); C(1;2)

c: A(-1;0); B(3;0); C(1;2)

\(AB=\sqrt{\left(3+1\right)^2+\left(0-0\right)^2}=4\)

\(AC=\sqrt{\left(1+1\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)

\(BC=\sqrt{\left(1-3\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)

Chu vi tam giác ABC là:

\(P_{ABC}=AB+AC+BC=4+4\sqrt{2}\)

Xét ΔABC có \(CA^2+CB^2=AB^2\)

nên ΔCAB vuông tại C

Diện tích tam giác ABC là:

\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}2\sqrt{2}\cdot2\sqrt{2}=\dfrac{1}{2}\cdot8=4\)