Giải bài tập toán dạng: Chứng minh đẳng thức hình học dựa vào tính chất của tiếp tuyến
Cách chứng minh đẳng thức hình học dựa vào tính chất của tiếp tuyến
Chắc hẳn các bạn đã từng gặp phải những bài toán phức tạp liên quan đến việc chứng minh đẳng thức hình học dựa vào tính chất của tiếp tuyến. Bài học sau sẽ giúp các bạn hiểu rõ phương pháp giải và áp dụng vào thực hành.
Đầu tiên, chúng ta cần nắm vững hai khái niệm quan trọng: đường tròn nội tiếp tam giác và đường tròn bàng tiếp tam giác. Đường tròn nội tiếp tam giác tiếp xúc với ba cạnh của tam giác, tâm của nó là giao điểm của các đường phân giác trong của tam giác. Trong khi đó, đường tròn bàng tiếp tam giác tiếp xúc với một cạnh của tam giác và phần kéo dài của hai cạnh còn lại.
Khi chứng minh đẳng thức hình học dựa vào tính chất của tiếp tuyến, chúng ta thường thực hiện các bước sau:
- Xác định những đoạn tiếp tuyến bằng nhau.
- Đại số hóa hình học.
- Sử dụng phép tính cộng diện tích và phương pháp diện tích.
Ví dụ: Cho đường tròn nội tiếp tam giác ABC, tiếp xúc với AB, BC, CA tại D, E, F. Chứng minh rằng 2AD = AB + AC - BC.
Để giải bài toán này, chúng ta sẽ đặt AD = AF = x, BD = BE = y, CE = CF = z và thực hiện các phép tính tương ứng. Kết quả cuối cùng sẽ giúp chúng ta chứng minh đẳng thức cần thiết.
Hy vọng rằng bài học này sẽ giúp các bạn hiểu rõ hơn về cách giải bài toán dạng chứng minh đẳng thức hình học dựa vào tính chất của tiếp tuyến. Hãy thực hành nhiều để nắm vững phương pháp này và hoàn thiện kiến thức của mình. Chúc các bạn thành công!
Bài tập và hướng dẫn giải
1. Cho tam giác ABC có chu vi 2p ngoại tiếp (I, r) gọi a, b, c, ha, hb, hc theo thứ tự là độ dài và chiều cao tương ứng của các cạnh BC, CA, AB. Chứng minh rằng:
a, $\frac{1}{h_{a}}+\frac{1}{h_{b}}+\frac{1}{h_{c}}=\frac{1}{r}$
b, ha + hb + hc = 2pr($\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$)
2. Cho (I) nội tiếp tam giác ABC tiếp xúc với AB tại D. Chứng minh rằng tam giác ABC vuông tại C khi và chỉ khi CA.CB = 2DA.DB
3. Cho tam giác ABC, đường tròn Ia bàng tiếp trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC = a, CA = b, AB = c. Chứng minh rằng:
a, AE = AF = $\frac{a+b+c}{2}$
b, BE = $\frac{a+b-c}{2}$
c, CF = $\frac{c+a-b}{2}$
4. Cho nửa đường tròn tâm O đường kính AB. Kẻ các tiếp tuyến Ax, By của nửa đường tròn. Qua điểm M bất kì thuộc nửa đường tròn (M khác A và B) kẻ tiếp tuyến với nửa đường tròn cắt Ax, By theo thứ tự tại C và D.
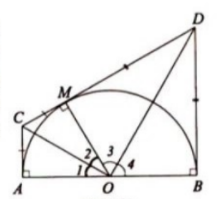
Chứng minh rằng:
a, $\widehat{COD}=90^{0}$
b, CD = AC + BD
c, Tích AC.BD không đổi khi M di chuyển trên nửa đường tròn.





