Đề học sinh giỏi tỉnh lớp 12 môn Toán năm 2022 2023 sở GD ĐT Bà Rịa Vũng Tàu

Nội dung Đề học sinh giỏi tỉnh lớp 12 môn Toán năm 2022 2023 sở GD ĐT Bà Rịa Vũng Tàu Bản PDF
-
Đề học sinh giỏi tỉnh lớp 12 môn Toán năm 2022-2023 sở GD ĐT Bà Rịa Vũng Tàu
Xin chào quý thầy cô và các em học sinh lớp 12! Dưới đây là đề thi chọn học sinh giỏi cấp tỉnh môn Toán lớp 12 năm học 2022-2023 do Sở Giáo dục và Đào tạo tỉnh Bà Rịa-Vũng Tàu tổ chức. Kỳ thi sẽ diễn ra vào ngày 13 tháng 12 năm 2022, với đề thi có đáp án và lời giải chi tiết được biên soạn bởi Nhóm Toán VDC & HSG THPT.
Trích dẫn một số câu hỏi trong đề thi:
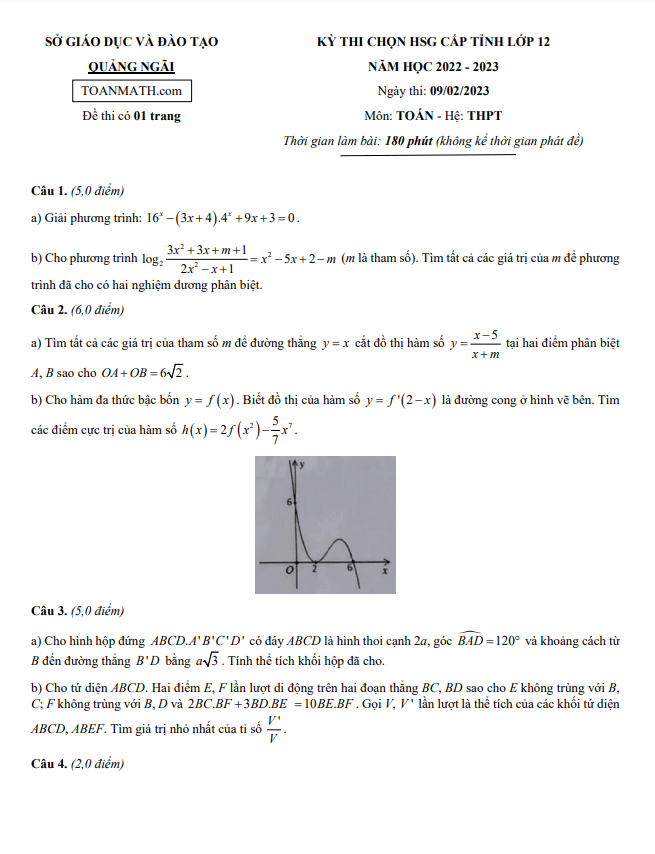
- Cho hàm số \(y = f(x) = 3x^2 - mx + \frac{m}{2}\) có đồ thị là \((C_m)\). Tìm tất cả các giá trị tham số \(m\) để \((C_m)\) cắt trục hoành tại 3 điểm phân biệt \(A(2;0)\), \(B\) và \(C\) sao cho trong hai điểm \(B\), \(C\) có một điểm nằm trong và một điểm nằm ngoài đường tròn \((x - 2)^2 + y^2 = 1\).
- Cho hình chóp \(S-ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\), tam giác \(SAC\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Gọi \(M\), \(N\) lần lượt là trung điểm của \(SA\) và \(BC\). Biết \(AB = a\) và \(MN\) tạo với mặt đáy một góc \(60°\). Tính thể tích khối chóp \(S-ABC\) theo \(a\).
- Cho hàm số \(f(x) = x - \cot(x) \sin(x) + \cos(x)\) xác định, liên tục trên \(\mathbb{R}\) và thoả mãn \(f(x) = x \cot(x) + \sin(x) \cos(x)\). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(g(x) = f(x)f'(x)\) trên đoạn \([-1;1]\).
Chúc quý thầy cô và các em học sinh có kỳ thi thành công! Hãy cố gắng hết mình và tự tin trả lời các câu hỏi trong đề thi.
X
Bình luận (0)
0.73556 sec| 2244.953 kb