Đề chọn đội tuyển HSG Toán năm 2020 sở GD ĐT Khánh Hòa (vòng 1).

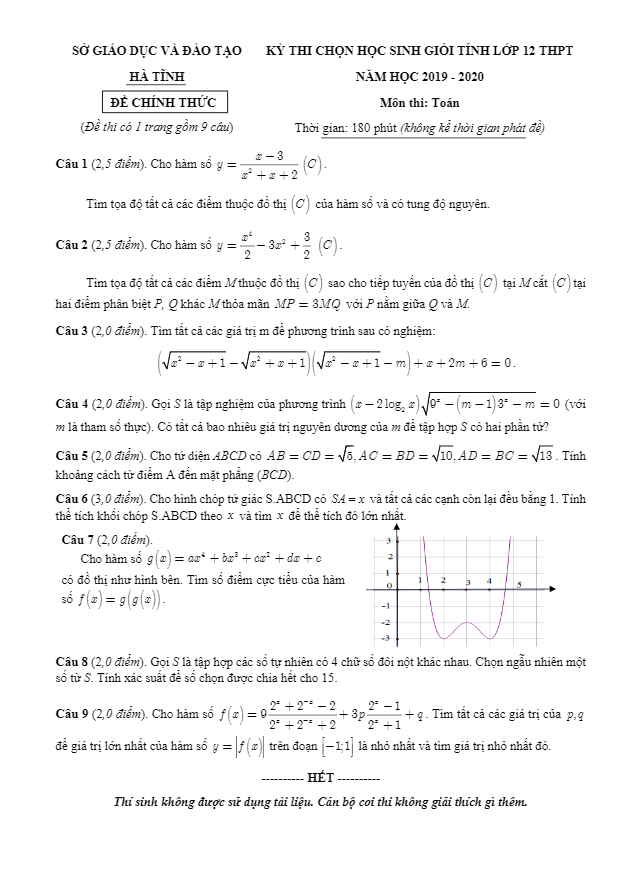
Nội dung Đề chọn đội tuyển HSG Toán năm 2020 sở GD ĐT Khánh Hòa (vòng 1). Bản PDF

Đề chọn đội tuyển HSG Toán năm 2020 sở GD&ĐT Khánh Hòa (vòng 1)

Ngày 19 tháng 09, sở Giáo dục và Đào tạo Khánh Hòa đã tổ chức kỳ thi chọn đội tuyển học sinh giỏi môn Toán cấp Quốc gia cho năm 2020. Đề chọn đội tuyển HSG Toán năm 2020 sở GD&ĐT Khánh Hòa (vòng 1) bao gồm 5 bài toán tự luận, thời gian làm bài được xác định là 180 phút. Dưới đây là một số câu hỏi đáng chú ý trong đề:

1. Chứng minh rằng với mỗi số nguyên dương n, luôn tồn tại một cặp số nguyên dương (a;b) duy nhất sao cho n = 1/2.(a + b – 1)(a + b – 2) + a.

2. Một nhóm phượt gồm n thành viên. Trong năm 2018, họ đã tổ chức sáu chuyến du lịch, mỗi chuyến có 5 thành viên tham gia và không có hai chuyến nào chung hơn 2 thành viên. Hãy tìm giá trị nhỏ nhất của n.

3. Cho tam giác ABC nhọn, không có đường trung tuyến AM và đường phân giác trong AD. Qua điểm N thuộc đoạn thẳng AD, kẻ NP vuông góc với AB. Đường thẳng qua P vuông góc với AD cắt đoạn thẳng AM tại Q. Hãy chứng minh rằng QN vuông góc với BC.

Đây là những câu hỏi đòi hỏi sự tỉ mỉ, suy luận logic và kiến thức sâu rộng về môn Toán. Hy vọng các thí sinh sẽ thể hiện tốt khả năng của mình trong kỳ thi này.