Câu 22: Trang 118 - sách giáo khoa (SGK) toán lớp 9 tập 2Hình 98 cho ta hình ảnh của một cái đồng...
Câu hỏi:
Câu 22: Trang 118 - sách giáo khoa (SGK) toán lớp 9 tập 2
Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo $(AO = OB)$.
Hãy so sánh tổng thể tích của hai hình nón và thể tích của hình trụ.
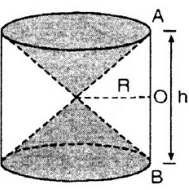
Hình 98
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Vương
Để so sánh tổng thể tích của hai hình nón và thể tích của hình trụ, ta cần tính thể tích của hai hình nón và thể tích của hình trụ.Cách 1:Thể tích của hai hình nón: $2.V_{nón} = 2 \times \frac{1}{3} \times \pi R^2 \times \frac{h}{2} = \frac{2}{3} \pi R^2 h$Thể tích của hình trụ: $V_{trụ} = \pi R^2 h$So sánh tổng thể tích của hai hình nón và thể tích của hình trụ:$\frac{2.V_{nón}}{V_{trụ}} = \frac{\frac{2}{3} \pi R^2 h}{\pi R^2 h} = \frac{2}{3} = 0.67$Từ đây, ta có $V_{trụ} = 0.67 \times 2.V_{nón} = 6.V_{nón}$Cách 2:Thể tích của hai hình nón: $2.V_{nón} = \frac{\pi R^2 h}{3}$Thể tích của hình trụ: $V_{trụ} = \pi R^2 h$So sánh tổng thể tích của hai hình nón và thể tích của hình trụ:$\frac{2.V_{nón}}{V_{trụ}} = \frac{\frac{\pi R^2 h}{3}}{\pi R^2 h} = \frac{1}{3}$Từ đó, ta có $V_{trụ} = \frac{1}{3} \times 2.V_{nón} = 6.V_{nón}$Vậy, tổng thể tích của hai hình nón bằng 1/6 thể tích của hình trụ.
Câu hỏi liên quan:
- Câu 15: Trang 117 - sách giáo khoa (SGK) toán lớp 9 tập 2Một hình nón được đặt vào bên trong một...
- Câu 16: Trang 117 - sách giáo khoa (SGK) toán lớp 9 tập 2Cắt mặt cắt xung quanh của một hình nón...
- Câu 17: Trang 117 - sách giáo khoa (SGK) toán lớp 9 tập 2Khi quay tam giác vuông để tạo ra một hình...
- Câu 18: Trang 117 - sách giáo khoa (SGK) toán lớp 9 tập 2Hình ABCD (h.95) khi quay quanh BC thì tạo...
- Câu 19: Trang 118 - sách giáo khoa (SGK) toán lớp 9 tập 2Hình khai triển của mặt xung quanh của một...
- Câu 20: Trang 118 - sách giáo khoa (SGK) toán lớp 9 tập 2Hãy điền đủ vào các ô trống ở bảng sau...
- Câu 21: Trang 118 - sách giáo khoa (SGK) toán lớp 9 tập 2Cái mũ của chú hề với các kích thước cho...
- Câu 23: Trang 119 - sách giáo khoa (SGK) toán lớp 9 tập 2Viết công thức tínhnửa góc ở...
- Câu 24: Trang 119 - sách giáo khoa (SGK) toán lớp 9 tập 2Hình khai triển của mặt xung quanh của một...
- Câu 25: Trang 119 - sách giáo khoa (SGK) toán lớp 9 tập 2Hãy tính diện tích xung quanh của hình nón...
- Câu 26: Trang 119 - sách giáo khoa (SGK) toán lớp 9 tập 2Hãy điền đủ vào các ô trống cho ở bảng sau...
- Câu 27:Trang 119 - sách giáo khoa (SGK) toán lớp 9 tập 2Một dụng cụ gồm một phần có dạng hình trụ,...
- Câu 28:Trang 120 - sách giáo khoa (SGK) toán lớp 9 tập 2Một cái xô bằng inox có dạng hình nón cụt...
- Câu 29: Trang 120 - sách giáo khoa (SGK) toán lớp 9 tập 2Cối xay gió của Đôn-ki-hô-tê (từ tác phẩm...





Với ví dụ trên, để so sánh tổng thể tích của hai hình nón và thể tích của hình trụ, cần xác định các giá trị cụ thể của bán kính và chiều cao để thực hiện phép tính.
Sau khi tính được tổng thể tích của hai hình nón và thể tích của hình trụ, ta so sánh hai giá trị để đưa ra kết luận về sự khác biệt của chúng.
Để tính thể tích của hình trụ, ta có công thức $V = \pi \times r^2 \times h$, trong đó r là bán kính đáy của hình trụ, h là chiều cao của hình trụ.
Khi tính thể tích của hai hình nón có cùng bán kính và chiều cao, ta cần nhân thể tích của một hình nón với 2.
Với hình nón trong hình 3D, ta có thể tính thể tích bằng công thức $V = \frac{1}{3} \times \pi \times r^2 \times h$, trong đó r là bán kính đáy của hình nón, h là chiều cao của hình nón.