BÀI TẬP3.17.Viết phương trình các đường chuẩn của các đường conic sau:
Câu hỏi:
BÀI TẬP
3.17. Viết phương trình các đường chuẩn của các đường conic sau:
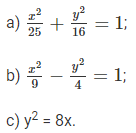
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Việt
Để tìm phương trình của các đường chuẩn của các đường conic, ta làm như sau:
a. Elip có phương trình $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ với a = 5, b = 4. Theo định nghĩa, đường chuẩn của elip là đường vuông góc với trục chính của elip tại các điểm tiếp xúc. Vì vậy, để tìm phương trình đường chuẩn, ta sử dụng công thức đường thẳng qua 2 điểm:
Phương trình đường chuẩn của elip là
$\dfrac{x}{5}\cos(\alpha) + \dfrac{y}{4}\sin(\alpha) = c$.
b. Hyperbol có phương trình $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ với a = 3, b = 2. Tương tự như trên, ta tìm được phương trình đường chuẩn của hyperbol là:
$\dfrac{x}{3}\cosh(\alpha) + \dfrac{y}{2}\sinh(\alpha) = c$.
c. Parabol có phương trình $y = ax^2$ với p = 4. Đường chuẩn của parabol là đường vuông góc với tiếp tuyến của parabol tại điểm tiếp xúc. Ta có phương trình đường chuẩn của parabol là:
$y - 8 + \dfrac{1}{8} = 0$.
a. Elip có phương trình $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ với a = 5, b = 4. Theo định nghĩa, đường chuẩn của elip là đường vuông góc với trục chính của elip tại các điểm tiếp xúc. Vì vậy, để tìm phương trình đường chuẩn, ta sử dụng công thức đường thẳng qua 2 điểm:
Phương trình đường chuẩn của elip là
$\dfrac{x}{5}\cos(\alpha) + \dfrac{y}{4}\sin(\alpha) = c$.
b. Hyperbol có phương trình $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ với a = 3, b = 2. Tương tự như trên, ta tìm được phương trình đường chuẩn của hyperbol là:
$\dfrac{x}{3}\cosh(\alpha) + \dfrac{y}{2}\sinh(\alpha) = c$.
c. Parabol có phương trình $y = ax^2$ với p = 4. Đường chuẩn của parabol là đường vuông góc với tiếp tuyến của parabol tại điểm tiếp xúc. Ta có phương trình đường chuẩn của parabol là:
$y - 8 + \dfrac{1}{8} = 0$.
Câu hỏi liên quan:
- 2.XÁC ĐỊNH ĐƯỜNG CONIC THEO TÂM SAI VÀ ĐƯỞNG CHUẨNLuyện tập 1:Lập phương trình đường conic biết tâm...
- Vận dụng 2: Hãy cho biếtquỹ đạo của từng vật thể trong bảng sau đây là parabol, elip hay...
- 3.18.Cho hai elipa) Tìm mối quan hệ giữa hai tâm sai của các elip đó.b) Chứng minh rằng...
- 3.19.Viết phương trình của đường conic có tâm sai bằng 1, tiêu điểm F(2; 0) và đường chuẩn là...
- 3.20.Quỹ đạo chuyển động của sao chổi Halley là một elip, nhận tâm Mặt Trời là một tiêu...
Bình luận (0)





